


Déclaration de types et filtrage de motif
Bien que les types prédéfinis d'Objective CAML permettent de construire des
données structurées, grâce aux n-uplets et aux listes, il est
nécessaire de pouvoir définir de nouveaux types pour décrire des
données structurées particulières. En Objective CAML, les déclarations
de type sont récursives et peuvent
être paramétrées par des variables de type, à la manière du type
'a list déjà rencontré. L'inférence de types tient compte de ces
nouvelles déclarations pour produire le type d'une expression. La
construction de valeurs de ces nouveaux types utilise les
constructeurs décrits dans leur définition. Une spécificité des
langages de la famille ML est le filtrage de motif. Il permet un
accès simple aux composants de structures de données complexes. La
définition d'une fonction correspond le plus souvent à un filtrage par
motif sur un de ses paramètres permettant une définition par cas de la
fonction.
Nous présentons tout d'abord le filtrage de motif sur les types
prédéfinis, pour ensuite décrire les différentes déclarations de
types structurés, la construction de telles valeurs ainsi que l'accès à leurs
composants par filtrage de motif.
Filtrage de motif (pattern matching)
Un motif, pattern en anglais, n'est pas à proprement parler une
expression d'Objective CAML. Il s'agit plutôt d'un assemblage correct
(syntaxiquement, et du point de vue des types) d'éléments tels que les
constantes des types de base (int, bool,
char, ..), les variables, les constructeurs et le symbole
_ dit motif universel. D'autres symboles servent à
l'écriture de motifs. Nous les introduirons au fur et à mesure des
besoins.
Le filtrage par motif s'applique aux valeurs. Il sert à
reconnaître la forme de cette valeur et permet d'orienter le
calcul en conséquence en associant à chaque motif une expression à
calculer.
Syntaxe
| match expr with |
| | p1 -> expr1 |
| : |
| | pn -> exprn |
L'expression expr est filtrée séquentiellement par les
différents motifs p1, ..., pn. Si un des
motifs (par exemple pi) est cohérent par rapport à la valeur de
expr alors la branche de calcul correspondante
(expri) est évaluée. Les différents motifs pi
sont du même type. Il en est de même pour les différentes expressions
expri. La barre verticale précédant le premier motif est
optionnelle.
Exemples
Voici deux façons de définir, par filtrage de motif, une fonction
imply de type (bool * bool) -> bool
implantant l'implication logique. Un motif pour les couples a la forme
( , ).
La première version de imply énumère tous les cas possibles
comme le ferait une table de vérité :
# let imply v = match v with
(true,true) -> true
| (true,false) -> false
| (false,true) -> true
| (false,false) -> true;;
val imply : bool * bool -> bool = <fun>
En utilisant des variables regroupant plusieurs cas, on obtient une
définition plus compacte.
# let imply v = match v with
(true,x) -> x
| (false,x) -> true;;
val imply : bool * bool -> bool = <fun>
Ces deux versions de imply calculent la même
fonction. C'est-à-dire qu'elles retournent les mêmes valeurs pour
les mêmes entrées.
Motif linéaire
Un motif doit être obligatoirement linéaire, c'est-à-dire
qu'une variable donnée ne peut y figurer au plus qu'une fois. Ainsi,
on aurait pu espérer pouvoir écrire :
# let equal c = match c with
(x,x) -> true
| (x,y) -> false;;
Characters 35-36:
This variable is bound several times in this matching
Mais cela aurait exigé du compilateur de savoir réaliser les tests
d'égalité. Or, la réalisation de tels tests soulève
immédiatement de nombreux problèmes. Si l'on se contente de
l'égalité physique entre valeurs, on obtient un système trop
faible, incapable de reconnaître l'égalité entre deux occurrences
de la liste [1; 2], par exemple. Si l'on décide d'utiliser une égalité
structurelle, on court le risque d'avoir à explorer, infiniment,
des structures circulaires. Les fonctions récursives, par exemple
sont des structures circulaires, mais on peut construire également
des valeurs récursives, donc circulaires, non fonctionnelles (voir
page ??).
Motif universel
Le symbole _ filtre toutes les valeurs possibles. Il est
appelé motif universel. Il peut être utilisé pour filtrer
des types complexes. On l'utilise, par exemple, pour simplifier encore
la définition de la fonction imply :
# let imply v = match v with
(true,false) -> false
| _ -> true;;
val imply : bool * bool -> bool = <fun>
Une définition par filtrage doit considérer l'ensemble des cas
possibles des valeurs filtrées. Si tel n'est pas le cas, le
compilateur affiche un message d'avertissement :
# let is_zero n = match n with 0 -> true ;;
Characters 17-40:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
1
val is_zero : int -> bool = <fun>
En effet si le l'argument d'appel est différent
de 0 la fonction ne sait pas quelle valeur retourner.
On peut alors compléter le filtrage en utilisant le motif universel.
# let is_zero n = match n with
0 -> true
| _ -> false ;;
val is_zero : int -> bool = <fun>
Si, à l'exécution, aucun motif n'est sélectionné, alors une exception
est déclenchée. Ainsi, on peut écrire :
# let f x = match x with 1 -> 3 ;;
Characters 11-30:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
0
val f : int -> int = <fun>
# f 1 ;;
- : int = 3
# f 4 ;;
Uncaught exception: Match_failure("", 11, 30)
L'exception Match_Failure est déclenchée à l'appel de
f 4, et si elle n'est pas récupérée entraîne
l'arrêt du calcul en cours (voir ??)
Combinaison de motifs
La combinaison de plusieurs motifs permet d'obtenir un nouveau motif qui
pourra déstructurer une valeur selon l'un ou l'autre de ses motifs
originaux. La forme syntaxique est la suivante :
Syntaxe
p1 | ...| pn
Elle construit un nouveau motif par combinaison des motifs p1,
...et pn. La seule contrainte forte est de refuser tout
nommage à l'intérieur de ces motifs. Donc chacun d'eux ne devra
contenir que des valeurs constantes ou le motif universel. L'exemple
suivant montre comment vérifier qu'un caractère est une
voyelle.
# let est_une_voyelle c = match c with
'a' | 'e' | 'i' | 'o' | 'u' | 'y' -> true
| _ -> false ;;
val est_une_voyelle : char -> bool = <fun>
# est_une_voyelle 'i' ;;
- : bool = true
# est_une_voyelle 'j' ;;
- : bool = false
Filtrage d'un paramètre
Le filtrage de motif est essentiellement utilisé pour la
définition de fonctions par cas. Pour alléger l'écriture de ces
définitions, la construction syntaxique function autorise le
filtrage d'un paramètre :
Syntaxe
| function |
| |
p1 -> expr1 |
| |
| |
p2 -> expr2 |
| |
|
: |
| |
| |
pn -> exprn |
La barre verticale précédant le premier motif est là aussi optionnelle.
En fait, tel Mr Jourdain, à chaque fois que nous définissons une
fonction, nous utilisons un filtrage de motif. En effet, la
construction function x -> expression ,
est une définition par filtrage utilisant un unique motif réduit
à une variable. On peut utiliser cette particularité avec des
motifs simples comme dans :
# let f = function (x,y) -> 2*x + 3*y + 4 ;;
val f : int * int -> int = <fun>
De fait la forme
function p1 -> expr1
| ...| pn -> exprn
est équivalente à
function expr -> match expr with
p1 -> expr1 | ...| pn -> exprn
En utilisant l'équivalence des déclarations mentionnée page
??, on écrira :
# let f (x,y) = 2*x + 3*y + 4 ;;
val f : int * int -> int = <fun>
Mais cette écriture naturelle n'est possible que si la valeur
filtrée appartient à un type n'ayant qu'un seul constructeur. Si
tel n'est pas le cas, le filtrage n'est pas exhaustif :
# let is_zero 0 = true ;;
Characters 13-21:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
1
val is_zero : int -> bool = <fun>
Nommage d'une valeur filtrée
Lors d'un filtrage de motif, il est parfois pratique de nommer tout ou
partie du motif. La forme syntaxique suivante introduit le mot clé
as qui associe un nom à un motif.
Syntaxe
( p as nom )
Ceci est utile lorsqu'on a besoin de déstructurer une valeur tout en
la conservant dans son intégralité. Dans l'exemple suivant, la
fonction min_rat rend le plus petit rationnel d'un couple de
rationnels. Ces derniers sont représentés par un couple numérateur et
dénominateur.
# let min_rat cr = match cr with
((_,0),c2) -> c2
| (c1,(_,0)) -> c1
| (((n1,d1) as r1), ((n2,d2) as r2)) ->
if (n1 * d2 ) < (n2 * d1) then r1 else r2;;
val min_rat : (int * int) * (int * int) -> int * int = <fun>
Pour comparer deux rationnels, il est nécessaire de les déstructurer
pour pouvoir nommer leur numérateur et leur dénominateur (n1,
n2, d1 et d2), mais il faut rendre le
couple initial (r1 ou r2). La construction as
nous permet ce nommage de parties d'une même valeur. Cela évite de
devoir reconstruire le rationnel retourné en résultat.
Filtrage avec gardes
Le filtrage avec gardes correspond à l'évaluation d'une expression
conditionnelle immédiatement après le filtrage d'un motif. Si cette
expression renvoie true, alors l'expression associée au motif
est évaluée, sinon le filtrage continue avec le motif suivant.
Syntaxe
| match expr with |
| : |
| | pi when condi -> expri |
| : |
L'exemple suivant utilise deux gardes pour tester l'égalité entre deux
rationnels.
# let eq_rat cr = match cr with
((_,0),(_,0)) -> true
| ((_,0),_) -> false
| (_,(_,0)) -> false
| ((n1,1), (n2,1)) when n1 = n2 -> true
| ((n1,d1), (n2,d2)) when ((n1 * d2) = (n2 * d1)) -> true
| _ -> false;;
val eq_rat : (int * int) * (int * int) -> bool = <fun>
Dans le filtrage du quatrième motif, si la garde échoue, le filtrage se
poursuit sur le cinquième motif.
Remarque
La vérification de l'exhaustivité du filtrage effectuée par
Objective CAML suppose que l'expression conditionnelle de la garde puisse
être fausse. En conséquence, elle ne tient pas compte de ce motif
puisqu'il n'est pas possible de savoir, avant l'exécution, si la garde
sera réalisée ou non.
L'exhaustivité du filtrage dans l'exemple suivant ne pourra pas être
détectée.
# let f = function x when x = x -> true;;
Characters 10-40:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
_
val f : 'a -> bool = <fun>
Filtrage d'intervalles de caractères
Dans le cadre du filtrage sur des caractères, il est fastidieux
de construire la combinaison de tous les motifs correspondant à un
intervalle de caractères. En effet, si l'on désire tester si un
caractère est bien une lettre, il faudra au minimum écrire 26 motifs
simples et les combiner. Objective CAML autorise pour les caractères,
l'écriture de motifs de la forme :
Syntaxe
'c1' .. 'cn'
Elle est équivalente à la combinaison :
'c1' | 'c2' | ...| 'cn'.
Par exemple le motif '0' .. '9' correspond au motif
'0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'. La
première forme est plus agréable à lire et plus rapide à écrire.
Warning
Ce trait fait partie des extensions du langage et pourra évoluer dans
les prochaines versions.
En utilisant les motifs combinés et les intervalles, on
définit une fonction discriminant les caractères selon plusieurs
critères.
# let char_discriminate c = match c with
'a' | 'e' | 'i' | 'o' | 'u' | 'y'
| 'A' | 'E' | 'I' | 'O' | 'U' | 'Y' -> "Voyelle"
| 'a'..'z' | 'A'..'Z' -> "Consonne"
| '0'..'9' -> "Chiffre"
| _ -> "Autre" ;;
val char_discriminate : char -> string = <fun>
On peut noter que l'ordre des ensembles de motifs a son importance. En
effet le second ensemble de motifs contient le premier, mais il n'est
examiné qu'après l'échec du premier.
Filtrage des listes
Comme nous l'avons vu, une liste peut être :
-
soit vide (la liste est de la forme []),
- soit composée d'un premier élément (sa tête) et d'une
sous-liste (sa queue). La liste est alors de la forme
t
::q.
Ces deux écritures possibles d'une liste sont utilisables comme des
motifs et permettent de filtrer une liste.
# let rec size x = match x with
[] -> 0
| _::queue_x -> 1 + (size queue_x) ;;
val size : 'a list -> int = <fun>
# size [];;
- : int = 0
# size [7;9;2;6];;
- : int = 4
On peut donc reprendre les exemples décrits précédemment (voir page
??) en utilisant le filtrage de motifs, comme par
exemple pour l'itération sur les listes.
# let rec fold_left f a = function
[] -> a
| tete::queue -> fold_left f (f a tete) queue ;;
val fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a = <fun>
# fold_left (+) 0 [8;4;10];;
- : int = 22
Déclaration de valeurs par filtrage d'un motif
La déclaration de valeurs utilise en fait le filtrage de motifs.
La déclaration let x = 18 filtre la valeur 18
avec le motif x. Tout motif est accepté comme filtre
d'une déclaration, les variables du motif sont
associées aux valeurs qu'elles filtrent.
# let (a,b,c) = (1, true, 'A');;
val a : int = 1
val b : bool = true
val c : char = 'A'
# let (d,c) = 8, 3 in d + c;;
- : int = 11
La portée des variables de filtrage est celle usuelle de la déclaration de valeurs
y compris pour les déclarations locales. Ici, c reste associée à la
valeur 'A'.
# a + (int_of_char c);;
- : int = 66
Comme tout filtrage, celui-ci peut ne pas être exhaustif.
# let [x;y;z] = [1;2;3];;
Characters 5-12:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
[]
val x : int = 1
val y : int = 2
val z : int = 3
# let [x;y;z] = [1;2;3;4];;
Characters 4-11:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
[]
Uncaught exception: Match_failure("", 4, 11)
Tout motif est accepté, y compris les constructeurs , le motif universel et les
motifs combinés.
# let tete :: 2 :: _ = [1; 2; 3] ;;
Characters 5-19:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
[]
val tete : int = 1
# let _ = 3. +. 0.14 in "PI" ;;
- : string = "PI"
Ce dernier exemple a peu d'intérêt dans le monde fonctionnel dans la mesure
où la valeur 3.14 calculée n'est pas nommée et donc perdue.
Déclaration de types
Les déclarations de type sont un autre constituant possible d'une
phrase Objective CAML. Elles permettent de définir de nouveaux types
correspondant aux structures de données originales utilisées dans un
programme. Il y a deux grandes familles de types : les types
produit pour les n-uplets ou les enregistrements ; les types
somme pour les unions.
Les déclarations de type utilisent le mot clé type.
Syntaxe
type nom = typedef ;;
À la différence des déclarations de variables, les déclarations de
types sont par défaut récursives. C'est-à-dire que les déclarations
de types, quand elles sont combinées, permettent de déclarer des types
mutuellement récursifs.
Syntaxe
| type |
nom1 |
= |
typedef1 |
| and |
nom2 |
= |
typedef2 |
| |
: |
|
|
| and |
nomn |
= |
typedefn ;; |
Les déclarations de types peuvent être paramétrées par des variables
de type. Un nom de variable de type commence toujours par une apostrophe
(caractère ') :
Syntaxe
type 'a nom = typedef ;;
Lorsqu'ils sont plusieurs, les paramètres de
types sont déclarés comme un n-uplet devant le nom du type :
Syntaxe
type
('a1 ...'an)
nom = typedef ;;
Seuls les paramètres de type définis dans la partie gauche de la
déclaration de type peuvent apparaître dans sa partie droite.
Remarque
L'afficheur de types d'Objective CAML renomme les paramètres de type
rencontrés, le premier se nomme 'a, le deuxième 'b
et ainsi de suite.
On peut toujours définir un nouveau type à partir d'un type ou
de plusieurs types existants.
Syntaxe
type nom = expression de type
Ceci est utile pour contraindre un type que l'on trouve trop
général.
# type 'param couple_entier = int * 'param ;;
type 'a couple_entier = int * 'a
# type couple_precis = float couple_entier ;;
type couple_precis = float couple_entier
Néanmoins sans contrainte sur les types, l'inférence produira le type le plus général.
# let x = (3, 3.14) ;;
val x : int * float = 3, 3.14
Mais on peut utiliser la contrainte de type pour voir apparaître le
nom désiré :
# let (x:couple_precis) = (3, 3.14) ;;
val x : couple_precis = 3, 3.14
Enregistrements
Les enregistrements sont des n-uplets dont chaque champ est nommé
à la manière des record de Pascal ou des struct
de C. Un enregistrement correspond toujours à la déclaration
d'un nouveau type. Un type enregistrement est défini par la
déclaration de son nom, du nom de chacun de ses champs et de leur type.
Syntaxe
type nom =
{ nom1 : t1;
...; nomn : tn
} ;;
On peut définir un type représentant les nombres complexes par :
# type complex = { re:float; im:float } ;;
type complex = { re: float; im: float }
La création d'une valeur de type enregistrement s'effectue en
donnant une valeur à chacun des champs (dans un ordre quelconque).
Syntaxe
{ nomi1 = expri1;
...; nomin = exprin
} ;;
Par exemple, on crée un nombre complexe de partie réelle
2. et de partie imaginaire 3. :
# let c = {re=2.;im=3.} ;;
val c : complex = {re=2; im=3}
# c = {im=3.;re=2.} ;;
- : bool = true
Dans le cas où des champs sont manquants, l'erreur suivante se produit :
# let d = { im=4. } ;;
Characters 9-18:
Some labels are undefined
L'accès à un champ est possible de deux façons : par la notation
pointée ou par le filtrage de certains champs.
La syntaxe de la notation pointée est usuelle :
Syntaxe
expr.nom
L'expression expr doit être d'un type enregistrement
possédant le champ nom.
Le filtrage d'un enregistrement permet de connaître la valeur
associée à un certain nombre de champs. Un motif de filtrage pour
un enregistrement a la syntaxe suivante :
Syntaxe
{ nomi = pi ;
...; nomj = pj }
Les motifs sont à droite du symbole = (pi, ...,
pj). Il n'est pas nécessaire de faire figurer tous les champs
d'un enregistrement dans un tel motif.
La fonction add_complex accède aux champs par la notation
pointée alors que la fonction mult_complex y accède par
filtrage.
# let add_complex c1 c2 = {re=c1.re+.c2.re; im=c1.im+.c2.im};;
val add_complex : complex -> complex -> complex = <fun>
# add_complex c c ;;
- : complex = {re=4; im=6}
# let mult_complex c1 c2 = match (c1,c2) with
({re=x1;im=y1},{re=x2;im=y2}) -> {re=x1*.x2-.y1*.y2;im=x1*.y2+.x2*.y1} ;;
val mult_complex : complex -> complex -> complex = <fun>
# mult_complex c c ;;
- : complex = {re=-5; im=12}
L'intérêt des enregistrements, par rapport aux n-uplets, est au
moins double :
-
une information descriptive et discriminante grâce aux noms des
champs : cela permet en particulier de simplifier les motifs de filtrage;
- un accès identique, par son nom, de n'importe quel champ
de l'enregistrement : l'ordre des champs n'a plus d'importance, seul
leur nom compte.
L'exemple suivant montre la facilité d'accès aux champs des
enregistrements par rapport au n-uplets :
# let a = (1,2,3) ;;
val a : int * int * int = 1, 2, 3
# let f tr = match tr with x,_,_ -> x ;;
val f : 'a * 'b * 'c -> 'a = <fun>
# f a ;;
- : int = 1
# type triplet = {x1:int; x2:int; x3:int} ;;
type triplet = { x1: int; x2: int; x3: int }
# let b = {x1=1; x2=2; x3=3} ;;
val b : triplet = {x1=1; x2=2; x3=3}
# let g tr = tr.x1 ;;
val g : triplet -> int = <fun>
# g b ;;
- : int = 1
Pour le filtrage de motif, il n'est pas nécessaire d'indiquer tous les
champs de l'enregistrement à filtrer. Le type inféré est alors celui du dernier type enregistrement déclaré contenant ces
champs.
# let h tr = match tr with {x1=x} -> x;;
val h : triplet -> int = <fun>
# h b;;
- : int = 1
Il existe une construction permettant de créer un enregistrement
identique à un autre sauf pour quelques champs. C'est souvent utile
pour les enregistrements contenant de nombreux champs.
Syntaxe
{ nom with nomi= expri
; ...; nomj=exprj}
# let c = {b with x1=0} ;;
val c : triplet = {x1=0; x2=2; x3=3}
Une nouvelle copie de la valeur de b est créée où seul le
champ x1 a une nouvelle valeur.
Warning
Ce trait fait partie des extensions du langage et pourra évoluer dans
les prochaines versions.
Types somme
À la différence des n-uplets ou des enregistrements, qui correspondent
à un produit cartésien, la déclaration d'un type somme correspond à
une union d'ensembles. On regroupe dans un même type des types
différents (par exemple des entiers et des chaînes de caractères). Les
différents membres de la somme sont discriminés par des
constructeurs qui permettent d'une part, comme leur nom l'indique, de
construire les valeurs de ce type et d'autre part d'accéder aux composantes de ces valeurs grâce au filtrage de motif.
Appliquer un constructeur à un argument, c'est indiquer que la
valeur retournée appartient à ce nouveau type.
On déclare un type somme en donnant le nom de ses constructeurs et
le type de leur éventuel argument.
Syntaxe
| type |
nom = ... |
| |
| Nomi ... |
| |
| Nomj of tj ... |
| |
| Nomk of tk * ...* tl
...;; |
Un nom de constructeur est un identificateur particulier :
Un nom de constructeur est un identificateur particulier :
Warning
Les noms des constructeurs commencent toujours par une majuscule.
Constructeurs constants
On appelle constructeur constant un constructeur qui n'attend
pas d'argument. Les constructeurs constants peuvent être par la
suite utilisés directement comme valeur du langage, comme une
constante.
# type piece = Pile | Face;;
type piece = | Pile | Face
# Pile;;
- : piece = Pile
Le type bool peut se définir de cette manière.
Constructeurs avec arguments
Les constructeurs peuvent avoir des arguments. Le mot clé of
indique le type des arguments du constructeur. Cela permet de
regrouper sous un même type des objets de types différents, chacun
étant introduit avec un constructeur particulier.
Voici un exemple classique de définition d'un type de données pour
représenter les cartes dans un jeu, ici le Tarot. On définit les types
couleur et carte de la manière suivante :
# type couleur = Pique | Coeur | Carreau | Trefle ;;
# type carte =
Roi of couleur
| Dame of couleur
| Cavalier of couleur
| Valet of couleur
| Petite_carte of couleur * int
| Atout of int
| Excuse ;;
La création d'une valeur du type carte s'effectue par
application d'un constructeur à une valeur de son type.
# Roi Pique ;;
- : carte = Roi Pique
# Petite_carte(Coeur, 10) ;;
- : carte = Petite_carte (Coeur, 10)
# Atout 21 ;;
- : carte = Atout 21
Et voici, par exemple, la fonction toutes_les_cartes qui
construit la liste de toutes les cartes d'une couleur passée en
argument.
# let rec interval a b = if a = b then [b] else a::(interval (a+1) b) ;;
val interval : int -> int -> int list = <fun>
# let toutes_les_cartes s =
let les_figures = [ Valet s; Cavalier s; Dame s; Roi s ]
and les_autres = List.map (function n -> Petite_carte(s,n)) (interval 1 10)
in les_figures @ les_autres ;;
val toutes_les_cartes : couleur -> carte list = <fun>
# toutes_les_cartes Coeur ;;
- : carte list =
[Valet Coeur; Cavalier Coeur; Dame Coeur; Roi Coeur; Petite_carte (Coeur, 1);
Petite_carte (Coeur, 2); Petite_carte (Coeur, 3); Petite_carte (Coeur, ...);
...]
Pour manipuler les valeurs des types somme, on utilise le filtrage de
motif. L'exemple suivant construit les fonctions de conversion de
valeurs de type couleur et de type carte en
chaînes de caractères (type string) :
# let string_of_couleur = function
Pique -> "pique"
| Carreau -> "carreau"
| Coeur -> "coeur"
| Trefle -> "trèfle" ;;
val string_of_couleur : couleur -> string = <fun>
# let string_of_carte = function
Roi c -> "roi de " ^ (string_of_couleur c)
| Dame c -> "dame de " ^ (string_of_couleur c)
| Valet c -> "valet de " ^ (string_of_couleur c)
| Cavalier c -> "cavalier de " ^ (string_of_couleur c)
| Petite_carte (c, n) -> (string_of_int n) ^ " de "^(string_of_couleur c)
| Atout n -> (string_of_int n) ^ " d'atout"
| Excuse -> "excuse" ;;
val string_of_carte : carte -> string = <fun>
L'alignement des motifs permet une lecture aisée de ces fonctions.
Le constructeur Petite_carte est considéré comme un constructeur à deux arguments. Le filtrage d'une telle valeur nécessite de nommer ses deux composants.
# let est_petite_carte c = match c with
Petite_carte v -> true
| _ -> false;;
Characters 45-59:
The constructor Petite_carte expects 2 argument(s),
but is here applied to 1 argument(s)
Pour éviter de devoir nommer chaque composant d'un constructeur,
on le déclare en ayant un seul argument en parenthésant le type n-uplet associé.
Le filtrage des deux constructeurs suivants diffère.
# type t =
C of int * bool
| D of (int * bool) ;;
# let acces v = match v with
C (i, b) -> i,b
| D x -> x;;
val acces : t -> int * bool = <fun>
Types récursifs
La définition de types récursifs est indispensable à tout
langage algorithmique pour décrire les structures de données
usuelles (listes, piles, arbres, graphes, etc. ). Pour cela, la
définition de types (type) est en Objective CAML par défaut
récursive, à la différence de la déclaration de valeurs
(let).
Le type des listes prédéfini en Objective CAML n'admet qu'un seul
paramètre. On peut vouloir, dans une structure de liste, stocker des
valeurs appartenant à deux types différents, par exemple, des
entiers (int) ou des caractères (char). Dans ce
cas, on définit :
# type int_or_char_list =
Nil
| Int_cons of int * int_or_char_list
| Char_cons of char * int_or_char_list ;;
# let l1 = Char_cons ( '=', Int_cons(5, Nil) ) in
Int_cons ( 2, Char_cons ( '+', Int_cons(3, l1) ) ) ;;
- : int_or_char_list =
Int_cons (2, Char_cons ('+', Int_cons (3, Char_cons ('=', Int_cons (...)))))
Types paramétrés
Un utilisateur peut également déclarer des types
avec paramètres. Ceci permet de généraliser l'exemple des listes
contenant des valeurs de deux types différents.
# type ('a, 'b) list2 =
Nil
| Acons of 'a * ('a, 'b) list2
| Bcons of 'b * ('a, 'b) list2 ;;
# Acons(2, Bcons('+', Acons(3, Bcons('=', Acons(5, Nil))))) ;;
- : (int, char) list2 =
Acons (2, Bcons ('+', Acons (3, Bcons ('=', Acons (...)))))
On peut, évidemment, instancier les paramètres 'a et
'b avec un même type.
# Acons(1, Bcons(2, Acons(3, Bcons(4, Nil)))) ;;
- : (int, int) list2 = Acons (1, Bcons (2, Acons (3, Bcons (4, Nil))))
Cette utilisation du type list2 peut, comme dans l'exemple
précédent, servir à marquer les entiers pairs et les entiers
impairs. On extrait alors la sous-liste des entiers pairs pour
construire une liste ordinaire.
# let rec extract_odd = function
Nil -> []
| Acons(_, x) -> extract_odd x
| Bcons(n, x) -> n::(extract_odd x) ;;
val extract_odd : ('a, 'b) list2 -> 'b list = <fun>
La définition de cette fonction ne donne aucune
indication sur la nature des valeurs stockées dans la
structure. C'est pourquoi son type est paramétré.
Portée des déclarations
Les noms de constructeurs obéissent à la même discipline de
portée que les déclarations globales : une redéfinition masque
l'ancienne. Néanmoins les valeurs d'un type masqué existent toujours.
La boucle d'interaction ne distinguera pas ces deux types à
l'affichage. D'où certains messages d'erreur peu clairs.
Dans ce premier exemple, le constructeur constant Nil du type
int_or_char a été masqué par la déclaration des
constructeurs du type ('a, 'b) list2.
# Int_cons(0, Nil) ;;
Characters 13-16:
This expression has type ('a, 'b) list2 but is here used with type
int_or_char_list
Ce deuxième exemple provoque un message d'erreur assez déroutant, du
moins la première fois qu'il apparaît. Soit le petit programme suivant :
# type t1 = Vide | Plein;;
type t1 = | Vide | Plein
# let vide_t1 x = match x with Vide -> true | Plein -> false ;;
val vide_t1 : t1 -> bool = <fun>
# vide_t1 Vide;;
- : bool = true
Ensuite, nous redéclarons le type t1 :
# type t1 = {u : int; v : int} ;;
type t1 = { u: int; v: int }
# let y = { u=2; v=3 } ;;
val y : t1 = {u=2; v=3}
Alors si l'on applique la fonction vide_t1 sur une valeur du nouveau type t1, on obtient le message d'erreur suivant :
# vide_t1 y;;
Characters 9-10:
This expression has type t1 but is here used with type t1
La première occurrence de t1 représente le premier type
défini alors que la deuxième correspond au deuxième type.
Types fonctionnels
Le type de l'argument d'un constructeur peut être quelconque. En
particulier, il peut tout aussi bien contenir le type d'une
fonction. Le type suivant construit des listes dont tous les éléments
sauf le dernier sont des valeurs fonctionnelles.
# type 'a listf =
Val of 'a
| Fun of ('a -> 'a) * 'a listf ;;
type 'a listf = | Val of 'a | Fun of ('a -> 'a) * 'a listf
Puisque les valeurs fonctionnelles sont des valeurs manipulables dans
le langage, on peut construire des valeurs de type listf :
# let huit_div = (/) 8 ;;
val huit_div : int -> int = <fun>
# let gl = Fun (succ, (Fun (huit_div, Val 4))) ;;
val gl : int listf = Fun (<fun>, Fun (<fun>, Val 4))
et des fonctions filtrant de telles valeurs :
# let rec compute = function
Val v -> v
| Fun(f, x) -> f (compute x) ;;
val compute : 'a listf -> 'a = <fun>
# compute gl;;
- : int = 3
Exemple : représentation des arbres
Les arbres sont des structures récurrentes en programmation. Les
types récursifs permettent de définir et manipuler facilement de
telles structures. Nous donnons dans ce paragraphe deux exemples de
structures arborescentes.
Arbres binaires
On définit une structure d'arbre binaire dont les noeuds sont
étiquetés par des valeurs d'un même type en déclarant :
# type 'a arbre_bin =
Empty
| Node of 'a arbre_bin * 'a * 'a arbre_bin ;;
On utilise cette structure pour définir un petit programme de tri
utilisant des arbres binaires de recherche. Un arbre binaire de
recherche a cette propriété que toutes les valeurs du fils gauche
sont inférieures à celle de la racine, et toutes celles du fils
droit lui sont supérieures. La figure 2.5 donne un exemple
d'une telle structure pour des entiers. Les noeuds vides (constructeur
Empty) y sont représentés par des petits carrés ; les
autres (constructeur Node), par un cercle où est inscrit la
valeur stockée.
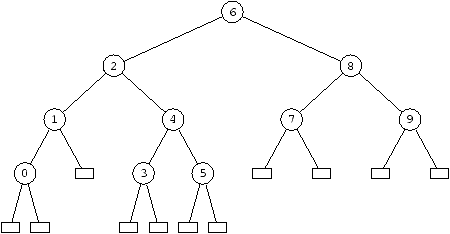
Figure 2.5 : Arbre binaire de recherche
On en extrait d'un arbre binaire de recherche une liste triée par un
parcours infixe effectuée par la fonction suivante :
# let rec list_of_arbre = function
Empty -> []
| Node(fg, r, fd) -> (list_of_arbre fg) @ (r :: (list_of_arbre fd)) ;;
val list_of_arbre : 'a arbre_bin -> 'a list = <fun>
Pour obtenir à partir d'une liste un arbre binaire de recherche, on
définit une fonction d'ajout.
# let rec ajout x = function
Empty -> Node(Empty, x, Empty)
| Node(fg, r, fd) -> if x < r then Node(ajout x fg, r, fd)
else Node(fg, r, ajout x fd) ;;
val ajout : 'a -> 'a arbre_bin -> 'a arbre_bin = <fun>
La fonction de transformation de liste en arbre s'obtient par
itération sur la liste de la fonction ajout.
# let rec arbre_of_list = function
[] -> Empty
| t::q -> ajout t (arbre_of_list q) ;;
val arbre_of_list : 'a list -> 'a arbre_bin = <fun>
La fonction de tri est alors simplement la composition des fonctions
arbre_of_list et list_of_arbre.
# let tri x = list_of_arbre (arbre_of_list x) ;;
val tri : 'a list -> 'a list = <fun>
# tri [5; 8; 2; 7; 1; 0; 3; 6; 9; 4] ;;
- : int list = [0; 1; 2; 3; 4; 5; 6; 7; 8; 9]
Arbres planaires généraux
Dans cette partie, nous utilisons les fonctions prédéfinies du
module List (voir page ??) suivantes :
-
List.map : qui applique une fonction à tous les
éléments d'une liste et retourne la liste des résultats;
- List.fold_left : qui est une version équivalente
de la fonction
fold_left définie page ??;
- List.exists qui applique une fonction à valeur
booléenne à tous les éléments d'une liste, si une de ces applications
vaut true alors le résultat est true, sinon la fonction
retourne false.
Un arbre planaire général est un arbre dont on ne fixe pas
a priori le nombre de fils : à chaque noeud on associe une
liste de fils dont la longueur peut varier.
# type 'a arbre = Empty
| Node of 'a * 'a arbre list ;;
L'arbre vide est représenté par la valeur Empty, une
feuille est un noeud sans fils soit de la forme
Node(x,[]), soit de la forme dégénérée
Node(x, [Empty;Empty; ..]). Il est alors relativement aisé
d'écrire des fonctions de manipulation de tels arbres comme
l'appartenance d'un élément à un arbre ou le calcul de la hauteur de
l'arbre.
Pour tester l'appartenance d'un élément e, on utilise
l'algorithme suivant : si l'arbre est vide alors e
n'appartient pas à cet arbre, sinon e appartient à l'arbre
si et seulement s'il est égal à l'étiquette de la racine, ou
s'il appartient à un des fils.
# let rec appartient e = function
Empty -> false
| Node(v, fs) -> (e=v) or (List.exists (appartient e) fs) ;;
val appartient : 'a -> 'a arbre -> bool = <fun>
Pour calculer la hauteur d'un arbre, on utilise la définition
suivante : un arbre vide est de hauteur 0 et sinon la hauteur de l'arbre est
égale à la hauteur du plus haut sous arbre augmentée de
1.
# let rec hauteur =
let max_list l = List.fold_left max 0 l in
function
Empty -> 0
| Node (_, fs) -> 1 + (max_list (List.map hauteur fs)) ;;
val hauteur : 'a arbre -> int = <fun>
Valeurs récursives non fonctionnelles
La déclaration récursive de valeurs non fonctionnelles permet de
construire des structures de données circulaires.
La déclaration suivante construit une liste circulaire à un
élément.
# let rec l = 1::l ;;
val l : int list =
[1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; ...]
L'application d'une fonction récursive sur une telle liste risque de
boucler jusqu'à saturation de la mémoire.
# size l ;;
Stack overflow during evaluation (looping recursion?).
L'égalité structurelle reste utilisable avec de telles listes
uniquement lorsque l'égalité physique est d'abord vérifiée :
# l=l ;;
- : bool = true
En revanche, si l'on définit une nouvelle liste, pourtant égale,
il ne faut pas utiliser le test d'égalité structurelle sous peine
de voir votre programme boucler indéfiniment. Nous ne recommandons
donc pas de tenter d'évaluer l'exemple suivant :
let rec l2 = 1::l2 in l=l2 ;;
Par contre, l'égalité physique reste toujours possible.
# let rec l2 = 1::l2 in l==l2 ;;
- : bool = false
Le prédicat == teste l'égalité d'une valeur immédiate
ou le partage d'un objet structuré (égalité sur l'adresse de la
valeur). Nous allons nous en servir pour vérifier qu'en explorant
une liste nous ne repassons pas par une sous-liste déjà
examinée. En premier lieu, nous définissons la fonction
memq qui vérifie la présence d'un élément dans une
liste en s'appuyant sur l'égalité physique. C'est le pendant de la
fonction
mem qui teste elle l'égalité structurelle; ces deux
fonctions appartiennent au module List.
# let rec memq a l = match l with
[] -> false
| b::l -> (a==b) or (memq a l) ;;
val memq : 'a -> 'a list -> bool = <fun>
La fonction de calcul de la taille est redéfinie en conservant la
liste des listes déjà examinées et en s'arrêtant si une liste
est rencontrée une seconde fois.
# let special_size l =
let rec size_aux previous l = match l with
[] -> 0
| _::l1 -> if memq l previous then 0
else 1 + (size_aux (l::previous) l1)
in size_aux [] l ;;
val special_size : 'a list -> int = <fun>
# special_size [1;2;3;4] ;;
- : int = 4
# special_size l ;;
- : int = 1
# let rec l1 = 1::2::l2 and l2 = 1::2::l1 in special_size l1 ;;
- : int = 4








