


Exercices
Fusion de deux listes
-
Écrire une fonction fusion_i
qui prend en entrée deux listes d'entiers triées en ordre croissant et
retourne une nouvelle liste triée contenant les éléments des deux
premières.
# let rec fusion_i l1 l2 = match (l1,l2) with
[],_ -> l2
| _,[] -> l1
| t1::q1,t2::q2 ->
if t1 < t2 then t1::(fusion_i q1 l2)
else t2::(fusion_i l1 q2);;
val fusion_i : 'a list -> 'a list -> 'a list = <fun>
- Écrire une fonction fusion
générale, qui prend en argument une fonction de
comparaison et deux listes triées selon cet ordre et retourne la
liste fusionnée selon le même ordre. La fonction de comparaison sera du type
'a -> 'a -> bool.
# let rec fusion f_ord l1 l2 = match (l1,l2) with
[],_ -> l2
| _,[] -> l1
| t1::q1,t2::q2 ->
if f_ord t1 t2 then t1::(fusion f_ord q1 l2)
else t2::(fusion f_ord l1 q2);;
val fusion : ('a -> 'a -> bool) -> 'a list -> 'a list -> 'a list = <fun>
- Appliquer
cette fonction à 2 listes d'entiers triées en ordre décroissant,
puis à deux listes de chaînes de caractères triées en ordre décroissant.
# fusion (>) [44;33;22;11] [55;30;10];;
- : int list = [55; 44; 33; 30; 22; 11; 10]
# fusion (<) ["mon"; "premier"; "programme"]
["bon";"essai";"numero";"un"];;
- : string list =
["bon"; "essai"; "mon"; "numero"; "premier"; "programme"; "un"]
- Que se passe-t-il
si une des listes ne respecte pas l'ordre donné?
Si au moins une des deux listes ne respecte pas l'ordre, alors le résultat
ne le respectera probablement pas.
- Écrire un nouveau type liste
sous la forme d'un enregistrement
contenant trois champs : la liste classique, une fonction d'ordre et un booléen indiquant si la liste respecte l'ordre.
# type 'a liste = {l: 'a list; f_ord : 'a -> 'a -> bool; r : bool};;
type 'a liste = { l: 'a list; f_ord: 'a -> 'a -> bool; r: bool }
- Écrire la fonction ajoute
qui ajoute un élément à une liste de ce type.
- Écrire une fonction
tri qui trie par insertion les éléments d'une liste.
# let ajoute e lt =
let rec ajoute_rec e l = match l with
[] -> [e]
| t::q -> if lt.f_ord e t then e::l
else t::(ajoute_rec e q)
in
if lt.r then {lt with l=ajoute_rec e lt.l}
else {lt with l = e::lt.l};;
val ajoute : 'a -> 'a liste -> 'a liste = <fun>
# let tri lt =
if lt.r then lt
else List.fold_right ajoute lt.l {l=[]; f_ord=lt.f_ord; r=true};;
val tri : 'a liste -> 'a liste = <fun>
- Écrire une nouvelle fonction fusion
pour ces listes.
# let rec fusion_lt l1 l2 =
if l1.f_ord <> l2.f_ord then failwith "ordre incompatible"
else
if l1.r then
if l2.r then {l = fusion l1.f_ord l1.l l2.l; f_ord = l1.f_ord; r = true}
else List.fold_right ajoute l2.l l1
else
if l2.r then fusion_lt l2 l1
else fusion_lt (tri l1) l2;;
val fusion_lt : 'a liste -> 'a liste -> 'a liste = <fun>
Arbres lexicaux
Pour la représentation de dictionnaires, on utilisera des arbres
lexicaux (ou tries).
# type noeud_lex = Lettre of char * bool * arbre_lex
and arbre_lex = noeud_lex list;;
# type mot = string;;
La valeur booléenne du noeud_lex marque la fin d'un mot
lorsqu'elle vaut true.
Dans une telle structure, la suite de mots << fa, far, faux, frise,
frit, frite >> est stockée de la façon suivante :
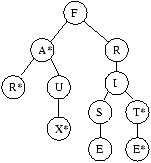
L'étoile (*) marque la fin d'un mot.
-
Écrire la fonction existe
qui teste si un mot appartient à un dictionnaire de type
arbre_lex.
# let rec existe m d =
let aux sm i n = match d with
[] -> false
| (Lettre (c,b,l))::q when c=sm.[i] ->
if n = 1 then b else existe (String.sub sm (i+1) (n-1)) l
| (Lettre (c,b,l))::q -> existe sm q
in aux m 0 (String.length m) ;;
val existe : string -> arbre_lex -> bool = <fun>
- Écrire une fonction ajoute
qui prend un mot et un dictionnaire
et retourne un nouveau dictionnaire qui contient ce mot en plus.
Si le mot existe déjà, il n'est pas nécessaire de l'ajouter.
# let rec ajoute m d =
let aux sm i n =
if n = 0 then d
else match d with
[] -> [Lettre (sm.[i], n = 1, ajoute (String.sub sm (i+1) (n-1)) [])]
| (Lettre(c,b,l))::q when c=sm.[i]->
if n = 1 then (Lettre(c,true,l))::q
else Lettre(c,b,ajoute (String.sub sm (i+1) (n-1)) l)::q
| (Lettre(c,b,l))::q -> (Lettre(c,b,l))::(ajoute sm q)
in aux m 0 (String.length m) ;;
val ajoute : string -> arbre_lex -> arbre_lex = <fun>
- Écrire une fonction construit
qui prend une liste de mots et construit le dictionnaire correspondant.
# let construit l =
let rec aux l d = match l with
[] -> d
| t::q -> aux q (ajoute t d)
in aux l [] ;;
val construit : string list -> arbre_lex = <fun>
- Écrire une fonction verifie
qui prend une liste de mots et un dictionnaire et retourne
la liste des mots n'appartenant pas à ce dictionnaire.
# let rec filter p = function
[] -> []
| t::q -> if p t then t::(filter p q) else filter p q ;;
val filter : ('a -> bool) -> 'a list -> 'a list = <fun>
# let verifie l d = filter (function x -> not (existe x d)) l ;;
val verifie : string list -> arbre_lex -> string list = <fun>
- Écrire une fonction selecte
qui prend un dictionnaire et une longueur
et retourne l'ensemble des mots de cette longueur.
# let string_of_char c = String.make 1 c ;;
val string_of_char : char -> string = <fun>
# let rec selecte n d = match d with
[] -> []
| (Lettre(c,b,l))::q when n=1 ->
let f (Lettre (c,b,_)) = if b then string_of_char c else "!" in
filter (function x -> x <> "!") (List.map f d)
| (Lettre(c,b,l))::q ->
let r1 = selecte (n-1) l
and r2 = selecte n q in
let pr = List.map (function s -> (string_of_char c)^s) r1 in
pr@r2 ;;
val selecte : int -> arbre_lex -> string list = <fun>
Parcours de graphes
On définit un type 'a graphe représentant les graphes
orientés par listes d'adjacence contenant pour chaque sommet la liste de ses successeurs :
# type 'a graphe = ( 'a * 'a list) list ;;
-
Écrire une fonction ajoute_som
qui ajoute un sommet à un graphe et retourne le nouveau graphe.
# let rec ajoute_som s g =
match g with
[] -> [(s,[])]
| (t,_)::_ when t=s -> failwith "sommet existant"
| sl::q -> sl::(ajoute_som s q) ;;
val ajoute_som : 'a -> ('a * 'b list) list -> ('a * 'b list) list = <fun>
# let ajoute_som = (ajoute_som : 'a -> 'a graphe -> 'a graphe) ;;
val ajoute_som : 'a -> 'a graphe -> 'a graphe = <fun>
- Écrire une fonction ajoute_arc
qui ajoute un arc à un graphe possédant déjà ces deux sommets.
# let rec ajoute_arc s1 s2 g =
match g with
[] -> failwith "sommet inconnu"
| (t,la)::q when t=s1 ->
if List.mem s2 la then failwith "arc existant"
else (s1,s2::la)::q
| sl::q -> sl::(ajoute_arc s1 s2 q) ;;
val ajoute_arc : 'a -> 'b -> ('a * 'b list) list -> ('a * 'b list) list =
<fun>
# let ajoute_arc = (ajoute_arc : 'a -> 'a -> 'a graphe -> 'a graphe ) ;;
val ajoute_arc : 'a -> 'a -> 'a graphe -> 'a graphe = <fun>
- Écrire une fonction arcs_dir
qui retourne tous les sommets accessibles à partir d'un sommet donné.
# let rec arcs_dir s g = match g with
[] -> []
| (t,la)::_ when t=s -> la
| _::q -> arcs_dir s q ;;
val arcs_dir : 'a -> ('a * 'b list) list -> 'b list = <fun>
# let arcs_dir = (arcs_dir : 'a -> 'a graphe -> 'a list) ;;
val arcs_dir : 'a -> 'a graphe -> 'a list = <fun>
- Écrire une fonction arcs_vers qui retourne
la liste de tous les sommets atteignant un sommet donné.
# let rec arcs_vers s g = match g with
[] -> []
| (t,la)::q -> if List.mem s la then t::(arcs_vers s q)
else (arcs_vers s q) ;;
val arcs_vers : 'a -> ('b * 'a list) list -> 'b list = <fun>
# let arcs_vers = (arcs_vers : 'a -> 'a graphe -> 'a list) ;;
val arcs_vers : 'a -> 'a graphe -> 'a list = <fun>










