Exercices
Coordonnées polaires
Les coordonnées de la bibliothèque Graphics sont
cartésiennes. Un segment y est représenté par son point de départ
(x0,y0) et son point d'arrivée (x1,y2) Il peut être
utile d'utiliser des coordonnées polaires. Un segment est alors décrit
par son point de départ (x0,y0) la taille du segment
(r) et son angle (a) Le rapport entre
coordonnées cartésiennes et coordonnées polaires est définie par les
équations :
|
|
ì
í
î |
|
| x1 |
= |
x0 + r * cos(a) |
| y1 |
= |
y0 + r * sin(a) |
|
|
# type seg_pol = {x:float; y:float; r:float; a:float};;
type seg_pol = { x: float; y: float; r: float; a: float }
-
Écrire la fonction to_cart
de transformation de coordonnées polaires
en coordonnées cartésiennes.
# let to_cart p =
(p.x,p.y),(p.x +. p.r *. (cos p.a), p.y +. p.r *. (sin p.a)) ;;
val to_cart : seg_pol -> (float * float) * (float * float) = <fun>
- Écrire la fonction draw_seg
qui affiche un segment défini en coordonnées polaires dans le
repère de Graphics.
# let draw_seg p =
let (x1,y1),(x2,y2) = to_cart p in
Graphics.moveto (int_of_float x1) (int_of_float y1);
Graphics.lineto (int_of_float x2) (int_of_float y2) ;;
val draw_seg : seg_pol -> unit = <fun>
- Un des intérêts des coordonnées polaires est de pouvoir facilement
appliquer des transformations sur un segment. Une translation ne
modifiera que le point de départ, une rotation sera uniquement
effectuée sur le champ angle, de même pour un changement d'échelle
sur le champ longueur. De façon générale, on peut
représenter une transformation comme un triplet de flottants : le
premier représente la translation (on ne considère, ici,
que des translations sur la droite du segment), le second la rotation
et le troisième le facteur d'échelle.
Définir la fonction app_trans
qui prend un segment en coordonnées polaires
et un triplet de transformations et retourne le nouveau segment.
# let app_trans seg ( da, dr, dxy ) =
let _,(x1,y1) = to_cart {seg with r = seg.r *. dxy} in
{x=x1; y=y1; a=seg.a +. da; r=seg.r *. dr} ;;
val app_trans : seg_pol -> float * float * float -> seg_pol = <fun>
- On peut construire des dessins récursifs par itération de
transformations. Écrire la fonction
dessin_r
qui prend en arguments un segment s, un
nombre d'itérations n, une liste de transformations
l et affiche tous les segments résultant des transformations sur s
itérées jusqu'à n.
# let rec dessin_r s n l =
if n = 0 then ()
else
begin
draw_seg s;
List.iter (fun t -> dessin_r (app_trans s t) (n-1) l) l
end ;;
val dessin_r : seg_pol -> int -> (float * float * float) list -> unit = <fun>
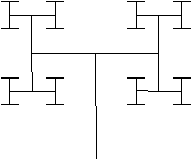
- Vérifier
que le programme suivant produit bien les images de la
figure 5.10.
let pi = 3.1415927 ;;
let s = {x=100.; y= 0.; a= pi /. 2.; r = 100.} ;;
dessin_r s 6 [ (-.pi/.2.),0.6,1.; (pi/.2.), 0.6,1.0] ;;
Graphics.clear_graph();;
dessin_r s 6 [(-.pi /. 6.), 0.6, 0.766;
(-.pi /. 4.), 0.55, 0.333;
(pi /. 3.), 0.4, 0.5 ] ;;
# Graphics.close_graph();;
- : unit = ()
# Graphics.open_graph ":0 200x200";;
- : unit = ()
# let pi = 3.1415927 ;;
val pi : float = 3.1415927
# let s = {x=100.; y= 0.; a= pi /. 2.; r = 100.} ;;
val s : seg_pol = {x=100; y=0; r=100; a=1.57079635}
# dessin_r s 6 [ (-.pi/.2.),0.6,1.; (pi/.2.), 0.6,1.0] ;;
- : unit = ()
# Graphics.clear_graph();;
- : unit = ()
# dessin_r s 6 [(-.pi /. 6.), 0.6, 0.766;
(-.pi /. 4.), 0.55, 0.333;
(pi /. 3.), 0.4, 0.5 ] ;;
- : unit = ()
Figure 5.10 : dessins récursifs
Éditeur de bitmaps
On cherche à un écrire un petit éditeur de bitmap (à la manière
de la commande bitmap de X-window). Pour cela on représente un
bitmap par ses dimensions (largeur et hauteur), la taille des pixels, et
un tableau à 2 dimensions de booléens.
-
Définir un type etat_bitmap
décrivant
l'information nécessaire pour conserver les valeurs des pixels, la
taille du bitmap et les couleurs d'affichage et d'effacement.
# type etat_bitmap =
{w : int; h : int; fg : Graphics.color; bg : Graphics.color;
pix : bool array array; s : int} ;;
type etat_bitmap =
{ w: int;
h: int;
fg: Graphics.color;
bg: Graphics.color;
pix: bool array array;
s: int }
- Écrire les fonctions de création d'un bitmap (create_bitmap)
et d'affichage d'un bitmap (draw_bitmap) .
# let create_bitmap x y f g t =
let r = Array.make_matrix x y false in
{ w = x; h = y; fg = f; bg = g; pix = r; s = t} ;;
val create_bitmap :
int -> int -> Graphics.color -> Graphics.color -> int -> etat_bitmap =
<fun>
# let draw_pix i j s c =
Graphics.set_color c;
Graphics.fill_rect (i*s+1) (j*s+1) (s-1) (s-1) ;;
val draw_pix : int -> int -> int -> Graphics.color -> unit = <fun>
# let draw_bitmap b =
for i=0 to b.w-1 do
for j=0 to b.h-1 do
draw_pix i j b.s (if b.pix.(i).(j) then b.fg else b.bg)
done
done ;;
val draw_bitmap : etat_bitmap -> unit = <fun>
- Écrire les fonctions read_bitmap
et write_bitmap
qui respectivement lit et écrit un bitmap dans un fichier passé en paramètre
en suivant le format ASCII de X-window. Si le fichier n'existe pas, alors la
fonction de lecture crée un nouveau bitmap en utilisant la fonction create_bitmap.
# let read_file filename =
let ic = open_in filename in
let rec aux () =
try
let line = (input_line ic) in
line :: (aux ())
with End_of_file -> close_in ic ; []
in aux ();;
val read_file : string -> string list = <fun>
# let read_bitmap filename =
let r = Array.of_list (read_file filename) in
let h = Array.length r in
let w = String.length r.(0) in
let b = create_bitmap w h Graphics.black Graphics.white 10 in
for j = 0 to h - 1 do
for i = 0 to w - 1 do
b.pix.(i).(j) <- ( r.(j).[i] = '#')
done
done;
b ;;
val read_bitmap : string -> etat_bitmap = <fun>
# let save_bitmap filename b =
let oc = open_out filename in
let f x = output_char oc (if x then '#' else '-') in
Array.iter (fun x -> (Array.iter f x); output_char oc '\n') b.pix ;
close_out oc ;;
val save_bitmap : string -> etat_bitmap -> unit = <fun>
Un pixel allumé est représenté par le caractère #,
l'absence d'un pixel par le caractère -. Chaque ligne de
caractères représente une ligne du bitmap. On pourra tester le
programme en utilisant les fonctions atobm et bmtoa de
X-window qui effectueront les conversions entre ce format ASCII et le
format des bitmaps créés par la commande bitmap. Voici
un exemple.
###################-------------#######---------######
###################---------------###-------------##--
###-----###-----###---------------###-------------#---
##------###------##----------------###-----------##---
#-------###-------#-----------------###---------##----
#-------###-------#-----------------###--------##-----
--------###--------------------------###-------#------
--------###-------###############-----###----##-------
--------###-------###---------###------###--##--------
--------###-------###----------##-------###-#---------
--------###-------###-----------#-------#####---------
--------###-------###-----------#--------###----------
--------###-------###--------------------####---------
--------###-------###--------------------####---------
--------###-------###------#-----------##---###-------
--------###-------###------#----------##----###-------
--------###-------##########----------#------###------
--------###-------##########---------##-------###-----
--------###-------###------#--------##--------###-----
--------###-------###------#-------##----------###----
--------###-------###--------------#------------###---
------#######-----###-----------#######--------#######
------------------###---------------------------------
------------------###-----------#---------------------
------------------###-----------#---------------------
------------------###----------##---------------------
------------------###---------###---------------------
------------------###############---------------------
- On reprend le squelette
de boucle d'interaction de la page ?? pour construire l'interface graphique
de l'éditeur. L'interface homme-machine est fort simple.
Le bitmap est affiché en permanence dans la fenêtre graphique.
Un clic souris sur une des cases du bitmap inverse sa valeur. Ce changement est répercuté
à l'écran. L'appui sur la touche 'S' sauve le bitmap dans le fichier. L'appui sur la touche 'Q'
fait sortir du programme.
-
Écrire la fonction start
de type etat_bitmap -> unit -> unit
qui ouvre la fenêtre graphique et affiche le bitmap passé en paramètre.
# exception Fin ;;
exception Fin
# let squel f_init f_end f_key f_mouse f_except =
f_init ();
try
while true do
try
let s = Graphics.wait_next_event
[Graphics.Button_down; Graphics.Key_pressed] in
if s.Graphics.keypressed
then f_key s.Graphics.key
else if s.Graphics.button
then f_mouse s.Graphics.mouse_x s.Graphics.mouse_y
with
Fin -> raise Fin
| e -> f_except e
done
with
Fin -> f_end () ;;
val squel :
(unit -> 'a) ->
(unit -> unit) ->
(char -> unit) -> (int -> int -> unit) -> (exn -> unit) -> unit = <fun>
# let start b () =
let ow = 1+b.w*b.s and oh = 1+b.h*b.s in
Graphics.open_graph (":0 " ^ (string_of_int ow) ^ "x" ^ (string_of_int oh)) ;
Graphics.set_color (Graphics.rgb 150 150 150) ;
Graphics.fill_rect 0 0 ow oh ;
draw_bitmap b ;;
val start : etat_bitmap -> unit -> unit = <fun>
- Écrire la fonction stop
qui ferme la fenêtre graphique et sort du programme.
# let stop () = Graphics.close_graph() ; exit 0 ;;
val stop : unit -> 'a = <fun>
- Écrire la fonction mouse
de type etat_bitmap -> int -> int -> unit
qui modifie l'état du pixel correspondant au clic souris
et affiche ce changement.
# let mouse b x y =
let i,j = (x / b.s),(y/b.s) in
if ( i < b.w ) && ( j < b.h) then
begin
b.pix.(i).(j) <- not b.pix.(i).(j) ;
draw_pix i j b.s (if b.pix.(i).(j) then b.fg else b.bg)
end ;;
val mouse : etat_bitmap -> int -> int -> unit = <fun>
- Écrire la fonction key
de type string -> etat_bitmap -> char -> unit
qui prend en paramètre un nom de fichier, un bitmap et le caractère de la touche appuyée
et effectue les actions associées : sauvegarde dans un fichier pour la touche 'S'
et déclenchement de l'exception Fin pour la touche 'Q'.
# let key filename b c =
match c with
'q' | 'Q' -> raise Fin
| 's' | 'S' -> save_bitmap filename b
| _ -> () ;;
val key : string -> etat_bitmap -> char -> unit = <fun>
- Écrire une fonction go
qui prend en paramètre un nom de fichier, charge le bitmap puis l'affiche
et lance la boucle d'interaction.
# let go name =
let b = try
read_bitmap name
with
_ -> create_bitmap 10 10 Graphics.black Graphics.white 10
in squel (start b) stop (key name b) (mouse b) (fun e -> ()) ;;
val go : string -> unit = <fun>
Ver de Terre
Le ver de terre est un petit organisme, longiforme, d'une certaine
taille qui va croître soit avec le temps soit en ramassant des objets
dans un monde. Le ver de terre est toujours en mouvement selon une
direction. Ses actions propres ou dirigées par un joueur permettent
uniquement un changement de direction. Le ver de terre disparaît s'il
touche un bord du monde ou s'il passe sur une partie de son corps. On
le représente le plus souvent par un vecteur de coordonnées avec deux
indices principaux : sa tête et sa queue. Un mouvement sera donc le
calcul des nouvelles coordonnées de sa tête, et son affichage, et
l'effacement de sa queue. Une croissance ne modifiera que sa tête sans
toucher à la queue du ver de terre.
-
Écrire le ou les types
Objective CAML pour représenter
un ver de terre et
le monde où il évolue.
On peut représenter un ver de terre par une file d'attente de ses coordonnées.
# type cell = Vide | Pleine ;;
type cell = | Vide | Pleine
# type monde = { l : int; h : int; cases : cell array array } ;;
type monde = { l: int; h: int; cases: cell array array }
# type vdt = { mutable tete : int; mutable queue : int; mutable taille : int;
mutable vx : int; mutable vy : int;
pos : (int * int) array } ;;
type vdt =
{ mutable tete: int;
mutable queue: int;
mutable taille: int;
mutable vx: int;
mutable vy: int;
pos: (int * int) array }
# type jeu = { m : monde; v : vdt; t_cell : int;
fg : Graphics.color; bg : Graphics.color } ;;
type jeu =
{ m: monde;
v: vdt;
t_cell: int;
fg: Graphics.color;
bg: Graphics.color }
- Écrire les fonctions d'initialisation
et d'affichage
d'un ver de terre dans un monde.
# let init_monde larg haut =
{ l = larg; h = haut; cases = Array.create_matrix larg haut Vide} ;;
val init_monde : int -> int -> monde = <fun>
# let init_vdt t t_max larg =
if t > larg then failwith "init_vdt"
else
begin
let v = { tete = t-1; queue = 0; taille = t; vx = 1; vy = 0;
pos = Array.create t_max (0,0) } in
let y = larg / 2
and rx = ref (larg/2 - t/2) in
for i=0 to t-1 do v.pos.(i) <- (!rx,y) ; incr rx done ;
v
end ;;
val init_vdt : int -> int -> int -> vdt = <fun>
# let init_jeu t t_max larg haut tc c1 c2 =
let j = { m = init_monde larg haut; v = init_vdt t t_max larg;
t_cell = tc; fg = c1; bg = c2 } in
for i=j.v.tete to j.v.queue do
let (x,y) = j.v.pos.(i) in
j.m.cases.(x).(y) <- Pleine
done ;
j ;;
val init_jeu :
int -> int -> int -> int -> int -> Graphics.color -> Graphics.color -> jeu =
<fun>
# let affiche_case x y t c =
Graphics.set_color c;
Graphics.fill_rect (x*t) (y*t) t t ;;
val affiche_case : int -> int -> int -> Graphics.color -> unit = <fun>
# let affiche_monde jeu =
let m = jeu.m in
for i=0 to m.l-1 do
for j=0 to m.h-1 do
let col = if m.cases.(i).(j) = Pleine then jeu.fg else jeu.bg in
affiche_case i j jeu.t_cell col
done
done ;;
val affiche_monde : jeu -> unit = <fun>
- Modifier la fonction squel
de squelette du programme
qui à chaque tour dans la boucle d'interaction effectue une action, paramétrée par une fonction.
La gestion de l'événement clavier ne doit pas
être bloquante.
(************** interaction **********)
# let tempo ti =
for i = 0 to ti do ignore (i * ti * ti ) done ;;
val tempo : int -> unit = <fun>
# exception Fin;;
exception Fin
# let squel f_init f_end f_key f_mouse f_except f_run =
f_init ();
try
while true do
try
tempo 200000 ;
if Graphics.key_pressed() then f_key (Graphics.read_key()) ;
f_run ()
with
Fin -> raise Fin
| e -> f_except e
done
with
Fin -> f_end () ;;
val squel :
(unit -> 'a) ->
(unit -> unit) ->
(char -> unit) -> 'b -> (exn -> 'c) -> (unit -> 'c) -> unit = <fun>
- Écrire la fonction run
qui fait avancer le ver de terre dans le jeu.
Cette fonction déclenche les exceptions Gagne (si le ver a atteint une certaine taille)
et Perdu s'il rencontre une case pleine ou un bord du monde.
# exception Perdu;;
exception Perdu
# exception Gagne;;
exception Gagne
# let run jeu temps itemps () =
incr temps;
let v = jeu.v in
let t = Array.length v.pos in
let ox,oy = v.pos.(v.tete) in
let nx,ny = ox+v.vx,oy+v.vy in
if (nx < 0 ) || (nx >= jeu.m.l) || (ny < 0) || (ny >= jeu.m.h)
then raise Perdu
else if jeu.m.cases.(nx).(ny) = Pleine then raise Perdu
else if v.tete = v.queue then raise Gagne
else
begin
let ntete = (v.tete + 1) mod t in
v.tete <- ntete ;
v.pos.(v.tete) <- (nx,ny);
jeu.m.cases.(nx).(ny) <- Pleine ;
affiche_case nx ny jeu.t_cell jeu.fg ;
if (!temps mod !itemps < (!itemps - 2)) then
begin
let qx,qy = v.pos.(v.queue) in
jeu.m.cases.(qx).(qy) <- Vide ;
affiche_case qx qy jeu.t_cell jeu.bg ;
v.queue <- (v.queue + 1) mod t
end
end ;;
val run : jeu -> int ref -> int ref -> unit -> unit = <fun>
- Écrire la fonction d'interaction
clavier qui modifie la direction du ver de terre.
# let key lact jeu c =
match c with
'q' | 'Q' -> raise Fin
| 'p' | 'P' -> ignore (Graphics.read_key ())
| '2' | '4' | '6' | '8' ->
let dx,dy = List.assoc c lact in
jeu.v.vx <- dx ;
jeu.v.vy <- dy
| _ -> () ;;
val key : (char * (int * int)) list -> jeu -> char -> unit = <fun>
- Écrire les autres fonctions utilitaires
de gestion de l'interaction et les passer au nouveau squelette de programme.
# let start jeu () =
let ow = jeu.t_cell * jeu.m.l and oh = jeu.t_cell * jeu.m.h in
let size = (string_of_int ow) ^ "x" ^ (string_of_int oh) in
Graphics.open_graph (":0 " ^ size) ;
Graphics.set_color (Graphics.rgb 150 150 150);
Graphics.fill_rect 0 0 ow oh;
affiche_monde jeu;
ignore (Graphics.read_key()) ;;
val start : jeu -> unit -> unit = <fun>
# let stop jeu () =
ignore (Graphics.read_key());
Graphics.close_graph() ;;
val stop : 'a -> unit -> unit = <fun>
# let mouse x y = () ;;
val mouse : 'a -> 'b -> unit = <fun>
# let except e = match e with
Perdu -> print_endline "PERDU"; raise Fin
| Gagne -> print_endline "GAGNE"; raise Fin
| e -> raise e ;;
val except : exn -> 'a = <fun>
- Écrire la fonction principale
de lancement de l'application.
# let la = [ ('2',(0,-1)) ; ('4',(-1,0)) ; ('6',(1,0)) ; ('8',(0,1)) ] ;;
val la : (char * (int * int)) list =
['2', (0, -1); '4', (-1, 0); '6', (1, 0); '8', (0, ...)]
# let go larg haut tc =
let col = Graphics.rgb 150 150 150 in
let jeu = init_jeu 5 (larg*haut /2) larg haut tc Graphics.black col in
squel (start jeu) (stop jeu) (key la jeu) mouse except (run jeu (ref 0) (ref 100));;
val go : int -> int -> int -> unit = <fun>