Récupération automatique
On distingue deux classes d'algorithmes de récupération automatique de
mémoire :
-
les compteurs de références : chaque zone allouée connaît le
nombre de références sur elle-même. Quand ce nombre vaut zéro, la zone
est libérée.
- les algorithmes explorateurs : à partir d'un ensemble de
racines (pointeurs), l'ensemble des valeurs accessibles
est exploré à la manière d'un parcours de graphe orienté.
Ce sont les algorithmes explorateurs qui sont le plus utilisés dans
les langages de programmation. En effet, un GC à compteur de
référence alourdi le traitement (mise à jour des
compteurs) même lorsqu'il n'y a pas besoin de récupérer quoique
ce soit.
Compteurs de références
On associe à chaque zone allouée un compteur. Ce compteur indique le
nombre de pointeurs sur cet objet. Il est incrémenté à chaque partage
de l'objet. Il est décrémenté quand un pointeur sur cet objet
disparaît. Quand ce compteur vaut 0, l'objet est récupéré.
L'avantage d'un tel système provient de la libération immédiate des
zones qui ne sont plus utilisées. Outre l'alourdissement
systématique des manipulations, les GC à compteurs de
références souffrent d'un autre inconvénient : ils ne savent pas
traiter les objets circulaires. Supposons qu'Objective CAML possède un tel
mécanisme. L'exemple suivant construit une valeur temporaire
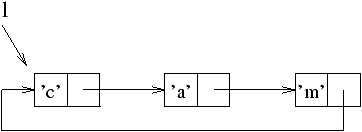
l, liste de caractères dont le dernier élément pointe sur la
cellule contenant 'c'. C'est donc bien une valeur circulaire
(figure 9.2).
# let rec l = 'c'::'a'::'m'::l in List.hd l ;;
- : char = 'c'
Figure 9.2 : représentation mémoire d'une liste circulaire
À la fin du calcul de cette expression, chaque élément de la
liste l a un compteur égal à un (même le premier car la
queue pointe sur la tête). Cette valeur n'est plus accessible et n'est
pourtant pas récupérée car son compteur de référence n'est pas
nul. Dans les langages munis d'une récupération par compteur de
références, comme le langage (Python), et autorisant la construction
de valeurs circulaires, il est nécessaire d'adjoindre un algorithme
explorateur de mémoire.
Algorithmes explorateurs
Les algorithmes explorateurs permettent à un instant donné d'explorer
le graphe des valeurs accessibles du tas. Cette exploration utilise un
ensemble de racines indiquant le début du parcours. Ces racines sont
extérieures au tas. Elles sont conservées le plus souvent dans une
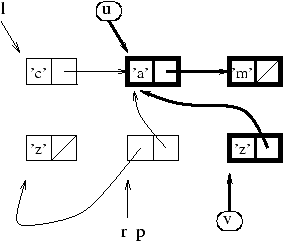
pile. Dans notre exemple de la figure 9.1, on peut
supposer que les valeurs de u et v font partie des
racines. Le parcours à partir de ces racines construira le graphe des
valeurs à conserver : les cellules et pointeurs en gras de la figure
9.3.
Figure 9.3 : récupération mémoire après un GC
Le parcours de ce graphe nécessite de savoir distinguer dans le tas
les valeurs immédiates de pointeurs. Si une racine pointe sur un
entier, il ne faut pas considérer cette valeur comme l'adresse d'une
autre cellule. Dans les langages fonctionnels, cette distinction est
obtenue en utilisant quelques bits des cellules du tas. On parle
alors de bits d'étiquette (en anglais
tag). C'est pourquoi les entiers d'Objective CAML n'utilisent que 31
bits. Cette option est décrite au chapitre 12, page
??. Il existe d'autres solutions au problème de
la distinction entre pointeurs et valeurs immédiates que nous
décrivons dans ce chapitre, page ??.
Les deux algorithmes les plus utilisés sont le Mark&Sweep,
qui construit la liste des cellules libres du tas, et
le Stop&Copy qui recopie les cellules encore vivantes dans
une deuxième zone mémoire.
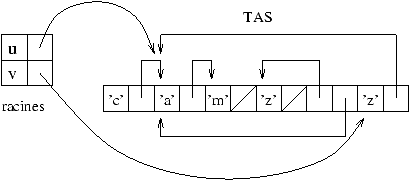
Le tas doit être vu comme un vecteur de cases mémoire. La
représentation de l'état du tas de l'exemple de la figure
9.1 est illustré à la figure 9.4.
Figure 9.4 : état du tas
On évalue un algorithme explorateur par les caractéristiques suivantes.
-
efficacité : la complexité en temps dépend-elle de la taille du tas
ou seulement de la taille des cellules vivantes ?
- facteur de récupération : toute la mémoire libre est-elle
disponible ?
- compaction : toute la mémoire libre est-elle disponible en un
seul bloc ?
- localisation : les différentes cellules d'une valeur structurée
sont-elles proches ?
- besoin de mémoire : l'algorithme nécessite-t'il d'utiliser une
partie de la mémoire lors de son déroulement ?
- déplacement des valeurs : les valeurs changent-elles de place suite à
une GC?
La localisation évite les changements de page mémoire pour le parcours
d'une valeur structurée. La compaction évite la fragmentation du tas
et autorise des allocations de la taille de la mémoire
disponible. L'efficacité, le facteur de récupération et les besoins
supplémentaires en mémoire sont intimement liés pour les complexités
en temps et en espace de l'algorithme.
Mark&Sweep
Le principe du Mark&Sweep est de tenir à jour une liste
des cellules libres du tas appelée freelist. Lors d'une
demande d'allocation, si la liste est vide ou s'il n'y a plus de
cellules libres d'une taille suffisante alors un Mark&Sweep
est effectué.
Il procède en deux étapes :
-
marquage des zones mémoires utiles à partir d'un ensemble de
racines (phase dite Mark) ;
- puis récupération des zones mémoire non marquées en parcourant
séquentiellement la totalité du tas (phase dite Sweep).
On peut illustrer la gestion mémoire du Mark&Sweep en utilisant quatre
<< colorations >> des cellules du tas : le blanc, le
gris1, le noir et le hachuré. La phase de marquage
utilise le noir et le gris ; la phase de récupération utilise le
hachuré et l'allocation, le blanc.
La signification des couleurs noir et gris utilisées par le marquage
est la suivante :
-
gris : cellule marquée dont les fils ne le sont pas encore ;
- noir : cellule marquée dont les fils immédiats le sont aussi.
Il sera nécessaire de conserver l'ensemble des cellules grisées pour
être sûr de tout explorer. À la fin du marquage chaque cellule est
blanche ou noire. Les cellules noires sont celles qui ont été
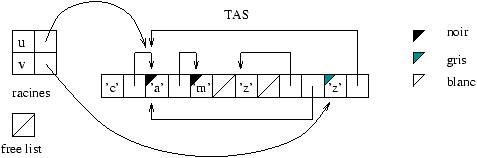
atteintes depuis les racines. La figure 9.5 montre une
étape intermédiaire du marquage pour l'exemple de la figure
9.4 : la racine u a été traitée et le
traitement de v en est à son début.
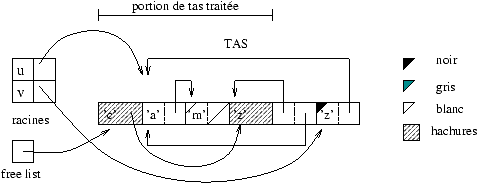
Figure 9.5 : phase de marquage
C'est dans la phase de récupération que la liste des cellules libres
est construite. Elle opère les modifications suivantes de
coloration :
-
noir devient blanc, la cellule vit ;
- blanc devient hachuré, la cellule est ajoutée à la
freelist.
La figure 9.6 montre l'évolution des couleurs du tas et la
construction de la freelist.
Figure 9.6 : phase de récupération
Les caractéristiques du Mark&Sweep sont les suivantes :
-
dépend de la taille entière du tas (étape Sweep) ;
- récupère toute la mémoire disponible ;
- ne compacte pas la mémoire ;
- n'assure pas la localisation ;
- ne déplace pas les données .
La phase de marquage est généralement implantée par une fonction
récursive. Elle utilise donc une partie de la pile d'exécution.
On peut donner une version entièrement itérative de
Mark&Sweep, n'utilisant pas une pile de profondeur inconnue, mais elle
s'avère moins efficace que la version en partie récursive.
Enfin, Mark&Sweep a besoin de connaître la taille des
valeurs. Celle-ci est soit conservée dans les valeurs, soit est
déduite des adresses mémoire par un découpage du tas en zone
d'allocation d'objets de taille bornée. Cet algorithme, implanté
dès les premiers Lisp, est encore largement utilisé. Une partie du
GC d'Objective CAML utilise un tel algorithme.
Stop&Copy
L'idée principale de ce GC est d'utiliser une mémoire secondaire pour
recopier et compacter les zones mémoire à conserver. Le tas est divisé
en deux parties : la zone utile (appelée from-space) et la zone
de recopie (appelée to-space).
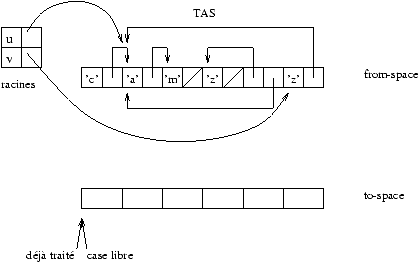
Figure 9.7 : début du Stop&Copy
L'algorithme est le suivant.
À partir d'un ensemble de racines, on recopie la partie utile de la zone
from-space dans l'espace to-space; la nouvelle adresse
d'une valeur déplacée est conservée (le plus souvent dans son
ancienne localisation) afin de mettre à jour toutes les autres valeurs
pointant sur cette valeur.
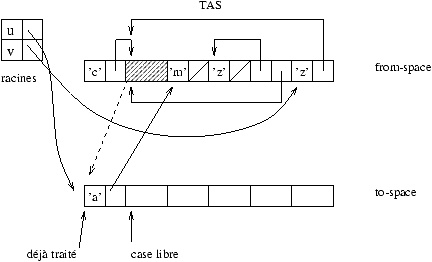
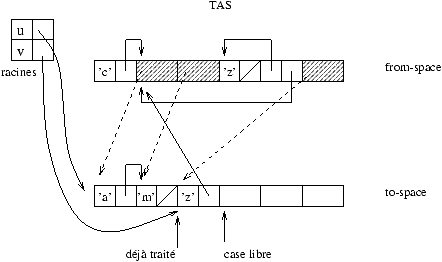
Figure 9.8 : recopie de from-space dans to-space
Le contenu des cellules recopiées forme les nouvelles racines. Tant que toutes ne sont pas traitées l'algorithme continue.
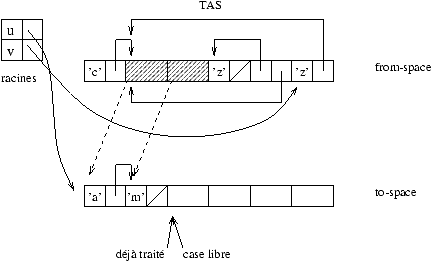
Figure 9.9 : nouvelles racines
En cas de partage, c'est-à-dire le déplacement d'une valeur déjà
déplacée, on se contente de donner la nouvelle adresse.
Figure 9.10 : partage
À la fin du GC, toutes les racines sont mises à jour pour
pointer sur les nouvelles adresses. Enfin, les rôles des deux zones sont
inversés en perspective du prochain GC.
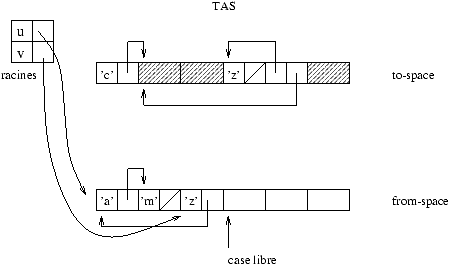
Figure 9.11 : inversion des zones
Les principales caractéristiques de ce GC sont les suivantes :
-
dépend uniquement de la taille des objets à conserver;
- seule la moitié de la mémoire est disponible;
- compacte la mémoire;
- possibilité de localisation (parcours en largeur);
- n'utilise pas de mémoire supplémentaire (from-space+to-space);
- algorithme non récursif;
- déplace les données dans la nouvelle zone mémoire;
Autres GC
Bien d'autres techniques, souvent issues des deux précédentes, ont été
utilisées soit dans des applications particulières, comme par exemple
la manipulation de grandes matrices en calcul formel, soit de manière
générale et liée à des techniques de compilation. Les GC à générations
permettent d'optimiser les techniques selon l'âge des valeurs. Les GC
à racines ambiguës sont utilisés quand on ne différencie pas
explicitement les valeurs immédiates des pointeurs (par exemple
lorsqu'on compile vers C). Enfin les GC incrémentiels permettent
d'éviter un ralentissement perceptible lors du déclenchement du GC.
GC à génération
Les programmes fonctionnels sont des programmes qui allouent en
général beaucoup et on constate que de très nombreuses valeurs ont
une durée de vie très courte2. D'autre part, dès qu'une valeur a survécu à
plusieurs GC, elle a de grandes chances d'exister pour un bon
moment. Pour éviter le parcours complet du tas, comme dans un
Mark&Sweep, à chaque récupération de mémoire, on souhaite
pouvoir n'effectuer un GC uniquement sur les valeurs ayant survécu à
1 ou quelques GC (c'est-à-dire des valeurs jeunes). C'est le plus
souvent dans ces espaces mémoire que l'on récupérera le plus de place.
Pour cela les objets sont datés, soit par une marque de temps, soit
par le nombre de GC auxquels ils ont survécu. Pour optimiser le GC on
utilisera des algorithmes différents selon l'âge des valeurs :
-
Les GC sur les objets jeunes devront être rapides et ne parcourir que
les jeunes générations.
-
Les GC sur les objets anciens devront être rares et bien récupérer
l'ensemble de la mémoire.
Une valeur qui vieillit sera de moins en moins partie prenante pour
les GC les plus fréquents. La difficulté provient alors de ne pouvoir
tenir compte uniquement de la partie mémoire des objets jeunes. Dans
un langage fonctionnel pur, c'est-à-dire sans modification physique,
les objets jeunes référencent des objets anciens par contre les objets
anciens ne possèdent pas de pointeurs vers les objets jeunes, car ils
ont été créés précédemment. Donc ces techniques s'y prêtent bien à l'exception
des langages à évaluation retardée qui en fait peuvent calculer les
composants d'une structure après celle-ci. Par
contre pour les langages fonctionnels avec modifications physiques, il
est toujours possible d'affecter une partie d'un objet ancien avec un
objet jeune. Le problème est alors de conserver une zone mémoire jeune
uniquement référencée par une valeur ancienne. Pour cela il sera
nécessaire de tenir à jour une table des références des objets anciens
vers les objets jeunes, pour obtenir un GC correct. On étudiera dans
la section suivante le cas d'Objective CAML.
GC à racines ambiguës
Jusqu'à maintenant, toutes les techniques de GC supposaient savoir
discriminer une valeur immédiate d'un pointeur. Il est à noter que
dans les langages fonctionnels polymorphes paramétriques la
représentation des valeurs est uniforme et occupe en général un mot
mémoire3. C'est ce qui permet d'avoir un code
générique pour les fonctions polymorphes.
Cependant, cette restriction de l'espace des entiers peut ne pas
être acceptable. Dans ce cas, les GC à racines ambiguës
permettent d'éviter de marquer les objets valeurs immédiates comme
les entiers. Dans ce cas toutes les valeurs utilisent un mot mémoire
sans aucune marque. Pour éviter le parcours d'une zone mémoire à
partir d'une racine contenant un entier, on utilise un algorithme de
discrimination entre valeurs immédiates et pointeurs valides reposant
sur les deux observations suivantes :
-
les adresses de début et de fin de tas sont connues donc toute
valeur en dehors de ces bornes est une valeur immédiate;
- les objets alloués sont alignés sur une adresse de
mot. Toute valeur ne correspondant pas à un alignement correct sera
aussi considérée comme une valeur immédiate.
Ainsi toute valeur du tas valide du point de vue des adresses dans le
tas sera comptée comme pointeur du tas et le récupérateur mémoire
cherchera à conserver cette zone, y compris dans le cas où cette
valeur est, en fait, une valeur immédiate. Ce cas peut devenir fort
rare en utilisant des pages mémoire spécifiques selon la taille des
objets. Il n'est pas possible de garantir que tout le tas inutile sera
ainsi récupéré. C'est le défaut principal de cette technique. Mais on
reste sûr que seules sont récupérées des zones effectivement
inutilisées.
En règle générale, les GC à racines ambiguës sont conservatifs,
i.e. ils ne déplacent pas les objets. En effet, puisque le GC
considère certaines valeurs immédiates comme un pointeur, il
serait dommageable d'en changer la valeur. Néanmoins des
spécialisations peuvent être apportées dans la constitution de
l'ensemble des racines et permettent de déplacer une partie des zones
correspondant à des racines sûres.
Les techniques de GC à racines ambiguës sont souvent utilisées
quand on compile un langage fonctionnel vers le langage C, vu alors
comme un assembleur portable. Elles permettent d'utiliser les valeurs
immédiates C codées sur un mot mémoire.
GC incrémentiel
Un des reproches souvent fait aux GC est d'arrêter l'exécution du
programme en cours pendant un temps perceptible à l'utilisateur et non
borné. Le premier cas est gênant pour certaines applications. On peut
citer les jeux d'action rapide où l'arrêt du jeu pendant quelques
secondes est trop souvent source d'injustice pour le joueur,
l'exécution repart sans prévenir. Le deuxième cas est source de perte
de contrôle pour des applications devant traiter un certain nombre
d'événements dans un temps limité. C'est typiquement le cas pour des
programmes embarqués qui contrôlent un appareil physique, comme un
véhicule ou une machine outil. Ces applications temps réel, dans le
sens où l'application doit répondre dans un temps borné, évitent le
plus souvent d'utiliser des GC.
Les GC incrémentiels doivent pouvoir s'interrompre pendant l'une
quelconque de leurs phases de traitement et pouvoir repartir en
assurant la sûreté de la récupération. Ils permettent de traiter
de manière assez satisfaisante le premier cas et peuvent être utilisés
dans le deuxième cas en forçant une discipline de programmation qui
isole clairement les parties logicielles qui utilisent l'allocation dynamique
de celles qui ne l'utilisent pas.
Reprenons l'exemple du Mark&Sweep et voyons les adaptations
qu'il faut lui apporter pour le rendre incrémentiel. Il y en a
essentiellement deux :
-
comment être sûr d'avoir tout marqué pendant la phase de marquage ?
- comment allouer durant les phases de marquage ou de récupération ?
Si le Mark&Sweep est interrompu pendant la phase Mark,
il faut assurer que les cellules allouées entre l'interruption du
marquage et sa reprise ne serons pas indûment récupérées par
le Sweep qui va suivre. Pour cela, on marque, par anticipation,
en noir ou gris les cellules allouées pendant l'interruption.
Si le Mark&Sweep est interrompu pendant la phase Sweep, on peut procéder
de façon usuelle en remettant à blanc
les marques des cellules allouées. En effet, comme la phase Sweep
parcourt séquentiellement le tas, les cellules allouées
pendant l'interruption sont localisées avant le point de redémarrage
du Sweep, elles ne seront pas réexaminées avant le prochain cycle
du GC.
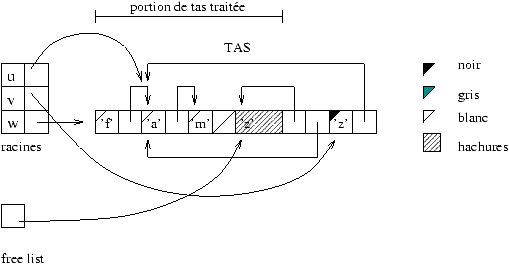
La figure 9.12 montre une allocation pendant la phase de
récupération. La racine w est créée par :
# let w = 'f'::v;;
val w : char list = ['f'; 'z'; 'a'; 'm']
Figure 9.12 : allocation pendant la récupération