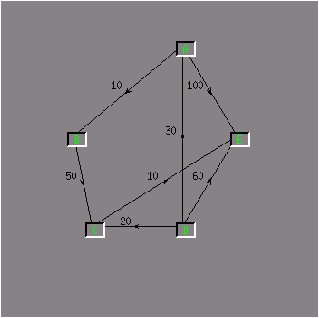
Figure 13.8 : Graphe de test



Le champ taille contient le nombre maximal de sommets et le champs ind, le nombre courant de sommets.
# typecout=Nan|Coutoffloat;;
# typemat_adj=coutarrayarray;;
# type'agraphe={mutableind:int;taille:int;sommets:'aarray;m:mat_adj};;
# letcree_graphest={ind=0;taille=t;sommets=Array.createts;m=Array.create_matrixttNan};;val cree_graphe : 'a -> int -> 'a graphe = <fun>
# letappartientsg=letrecauxi=(i<g.taille)&((g.sommets.(i)=s)or(aux(i+1)))inaux0;;val appartient : 'a -> 'a graphe -> bool = <fun>
# letindexsg=letrecauxi=ifi>=g.taillethenraiseNot_foundelseifg.sommets.(i)=sthenielseaux(i+1)inaux0;;val index : 'a -> 'a graphe -> int = <fun>
# letajoute_sommetsg=ifg.ind=g.taillethenfailwith"le graphe est plein"elseifappartientsgthenfailwith"le sommet existe déjà"else(g.sommets.(g.ind)<-s;g.ind<-g.ind+1);;val ajoute_sommet : 'a -> 'a graphe -> unit = <fun>
# letajoute_arcs1s2cg=tryletx=indexs1gandy=indexs2ging.m.(x).(y)<-CoutcwithNot_found->failwith"sommet inexistant";;val ajoute_arc : 'a -> 'a -> float -> 'a graphe -> unit = <fun>
# lettest_aho()=letg=cree_graphe"rien"5inList.iter(funx->ajoute_sommetxg)["A";"B";"C";"D";"E"];List.iter(fun(a,b,c)->ajoute_arcabcg)["A","B",10.;"A","D",30.;"A","E",100.0;"B","C",50.;"C","E",10.;"D","C",20.;"D","E",60.];fori=0tog.ind-1dog.m.(i).(i)<-Cout0.0done;g;;val test_aho : unit -> string graphe = <fun>
# leta=test_aho();;val a : string graphe ={ind=5; taille=5; sommets=[|"A"; "B"; "C"; "D"; "E"|];m=[|[|Cout 0; Cout 10; Nan; Cout 30; Cout ...|]; ...|]}

Figure 13.8 : Graphe de test
TAILLE 5 SOMMET A SOMMET B SOMMET C SOMMET D SOMMET E ARC A B 10.0 ARC A D 30.0 ARC A E 100.0 ARC B C 50. ARC C E 10. ARC D C 20. ARC D E 60.Pour analyser de tels fichiers, on utilise le module Genlex d'analyse lexicale. L'analyseur lexicale est construit à partir de la liste de mots clés keywords.
# letkeywords=["TAILLE";"SOMMET";"ARC";"#"];;val keywords : string list = ["TAILLE"; "SOMMET"; "ARC"; "#"]
# letlexer_linel=Genlex.make_lexerkeywords(Stream.of_stringl);;val lexer_line : string -> Genlex.token Stream.t = <fun>
# letparser_linegs=matchswithparser[<'(Genlex.Kwd"TAILLE");'(Genlex.Intn)>]->g:=cree_graphe""n|[<'(Genlex.Kwd"SOMMET");'(Genlex.Identnom)>]->ajoute_sommetnom!g|[<'(Genlex.Kwd"ARC");'(Genlex.Identn1);'(Genlex.Identn2);'(Genlex.Floatc)>]->ajoute_arcn1n2c!g|[<'(Genlex.Kwd"#")>]->()|[<>]->();;val parser_line : string graphe ref -> Genlex.token Stream.t -> unit = <fun>
L'appel suivant construit un graphe à partir du fichier aho.dat.
# letcreate_graphename=letg=ref{ind=0;taille=0;sommets=[||];m=[||]}inletic=open_innameintryprint_string("Loading "^name^": ");whiletruedoprint_string".";letl=input_lineicinparser_lineg(lexer_linel)done;!gwithEnd_of_file->print_newline();close_inic;!g;;val create_graphe : string -> string graphe = <fun>
# letb=create_graphe"PROGRAMMES/aho.dat";;Loading PROGRAMMES/aho.dat: ..............val b : string graphe ={ind=5; taille=5; sommets=[|"A"; "B"; "C"; "D"; "E"|];m=[|[|Nan; Cout 10; Nan; Cout 30; Cout 100|]; ...|]}
Le champ source contient le sommet de départ ; le champ deja_traites, les sommets dont on connaît déjà le chemin optimal à partir de la source et le champ nb, le nombre de sommets déjà traités. Le vecteur distances tient à jour les distances minimales entre la source et les autres sommets. Le vecteur chemin contient, pour chaque sommet, le sommet le précédent dans le chemin de moindre coût. On peut ainsi reconstituer un chemin de la source vers n'importe quel autre sommet.
# typeetat_recherche={chemins:intarray;deja_traites:boolarray;distances:coutarray;source:int;nb:int};;
# letcreer_etat()={chemins=[||];deja_traites=[||];distances=[||];nb=0;source=0};;
# letLa valeur Nan joue un rôle particulier dans les calculs et la comparaison. Nous y reviendrons lorsque nous aurons donné la fonction principale (voir page ??).a_coutc=matchcwithNan->false|_->true;;val a_cout : cout -> bool = <fun>
# letfloat_of_coutc=matchcwithNan->failwith"float_of_cout"|Coutx->x;;val float_of_cout : cout -> float = <fun>
# letadd_coutc1c2=match(c1,c2)withCoutx,Couty->Cout(x+.y)|Nan,Couty->c2|Coutx,Nan->c1|Nan,Nan->c1;;val add_cout : cout -> cout -> cout = <fun>
# letinf_coutc1c2=match(c1,c2)withCoutx,Couty->x<y|Coutx,Nan->true|_,_->false;;val inf_cout : cout -> cout -> bool = <fun>
# exceptionTrouveofint;;exception Trouve of int
# letpremier_non_traiteer=tryfori=0toer.nb-1doifnoter.deja_traites.(i)thenraise(Trouvei)done;raiseNot_found;0withTrouvei->i;;val premier_non_traite : etat_recherche -> int = <fun>
# letpp_non_traiteper=letsi=refpandsd=refer.distances.(p)infori=p+1toer.nb-1doifnoter.deja_traites.(i)thenifinf_couter.distances.(i)!sdthen(sd:=er.distances.(i);si:=i)done;!si,!sd;;val pp_non_traite : int -> etat_recherche -> int * cout = <fun>
# exceptionNo_way;;exception No_way
# letune_etapeerg=letp=premier_non_traiteerinletnp,nc=pp_non_traiteperinifnot(a_coutnc)thenraiseNo_wayelsebeginer.deja_traites.(np)<-true;fori=0toer.nb-1doifnoter.deja_traites.(i)thenifa_coutg.m.(np).(i)thenletic=add_couter.distances.(np)g.m.(np).(i)inifinf_couticer.distances.(i)then(er.chemins.(i)<-np;er.distances.(i)<-ic)done;erend;;val une_etape : etat_recherche -> 'a graphe -> etat_recherche = <fun>
# letdijsg=ifappartientsgthenbeginleti=indexsginleter={chemins=Array.createg.ind(-1);deja_traites=Array.createg.indfalse;distances=Array.createg.indNan;nb=g.ind;source=i}iner.deja_traites.(i)<-true;forj=0tog.ind-1doletc=g.m.(i).(j)iner.distances.(j)<-c;ifa_coutcthener.chemins.(j)<-idone;tryfork=0toer.nb-2doignore(une_etapeerg)done;erwithNo_way->erendelsefailwith"dij: sommet inconnu";;val dij : 'a -> 'a graphe -> etat_recherche = <fun>
# leta=test_aho();;
# letr=dij"A"a;;
# r.chemins;;- : int array = [|0; 0; 3; 0; 2|]
# r.distances;;- : cout array = [|Cout 0; Cout 10; Cout 50; Cout 30; Cout 60|]
Cette fonction récursive utilise la pile d'appel pour afficher dans le bon ordre les sommets. On note l'utilisation d'un format "a" pour conserver le polymorphisme des graphes y compris pour l'affichage, d'où le paramètre fonctionnel f.
# letaff_etatf(g,et)dest=ifappartientdestgthenletd=indexdestginletrecauxis=ifis=et.sourcethenPrintf.printf"%a"fg.sommets.(is)else(letold=et.chemins.(is)inauxold;Printf.printf" -> (%4.1f) %a"(float_of_coutg.m.(old).(is))fg.sommets.(is))inifnot(a_coutet.distances.(d))thenPrintf.printf"no way\n"else(auxd;Printf.printf" = %4.1f\n"(float_of_coutet.distances.(d)));;val aff_etat :(out_channel -> 'a -> unit) -> 'a graphe * etat_recherche -> 'a -> unit =<fun>
# aff_etat(funxy->Printf.printf"%s!"y)(a,r)"E";;A! -> (30.0) D! -> (20.0) C! -> (10.0) E! = 60.0- : unit = ()
Les champs g et w correspondent au graphe et au tableau de pointeurs faibles sur les états de recherche pour chaque source possible.
# type'arecherche_graphe={g:'agraphe;w:etat_rechercheWeak.t};;
# letcreate_rech_grapheg={g=g;w=Weak.createg.ind};;val create_rech_graphe : 'a graphe -> 'a recherche_graphe = <fun>
# letdij_rapidesrg=leti=indexsrg.ginmatchWeak.getrg.wiwithNone->leter=dijsrg.ginWeak.setrg.wi(Someer);er|Someer->er;;val dij_rapide : 'a -> 'a recherche_graphe -> etat_recherche = <fun>
# letrg_a=create_rech_grapheainletr=dij_rapide"A"rg_ainaff_etat(funxy->Printf.printf"%s!"y)(a,r)"E";;A! -> (30.0) D! -> (20.0) C! -> (10.0) E! = 60.0- : unit = ()
# letexe_timefgss=lett0=Sys.time()inPrintf.printf"Début (%5.2f)\n"t0;List.iter(funs->ignore(fsg))ss;lett1=Sys.time()inPrintf.printf"Fin (%5.2f)\n"t1;Printf.printf"Durée = (%5.2f)\n"(t1-.t0);;val exe_time : ('a -> 'b -> 'c) -> 'b -> 'a list -> unit = <fun>
# letss=letss0=ref[]inleti0=int_of_char'A'inletnew_si=Char.escaped(char_of_int(i0+i))infori=0to20000doss0:=(new_s(Random.inta.taille))::!ss0done;!ss0;;val ss : string list =["A"; "B"; "D"; "A"; "E"; "C"; "B"; "B"; "D"; "E"; "B"; "E"; "C"; "E"; "E";"D"; "D"; "A"; "E"; ...]
# Printf.printf"Fonction dij :\n";exe_timedijass;;Fonction dij :Début ( 7.08)Fin ( 8.02)Durée = ( 0.94)- : unit = ()
# Printf.printf"Fonction dij_rapide :\n";exe_timedij_rapide(create_rech_graphea)ss;;Fonction dij_rapide :Début ( 8.02)Fin ( 8.13)Durée = ( 0.11)- : unit = ()
##load"PROGRAMMES/upi.cmo";;
# type'agg={mutablesrc:'a*Upi.component;mutabledest:'a*Upi.component;pos:(int*int)array;rg:'arecherche_graphe;mutableetat:etat_recherche;mutablemain:Upi.component;to_string:'a->string;from_string:string->'a};;
# letcree_ggrgvpostsfs={src=rg.g.sommets.(0),Upi.empty_component;dest=rg.g.sommets.(0),Upi.empty_component;pos=vpos;rg=rg;etat=creer_etat();main=Upi.empty_component;to_string=ts;from_string=fs};;val cree_gg :'a recherche_graphe ->(int * int) array -> ('a -> string) -> (string -> 'a) -> 'a gg = <fun>
# letrotatela=letca=cosaandsa=sinainList.map(function(x,y)->(x*.ca+.-.y*.sa,x*.sa+.y*.ca))l;;val rotate : (float * float) list -> float -> (float * float) list = <fun>
# lettranslatel(tx,ty)=List.map(function(x,y)->(x+.tx,y+.ty))l;;val translate :(float * float) list -> float * float -> (float * float) list = <fun>
# letdisplay_arrow(mx,my)a=lettriangle=[(5.,0.);(-3.,3.);(1.,0.);(-3.,-3.);(5.,0.)]inlettr=rotatetriangleainletttr=translatetr(mx,my)inlettt=List.map(function(x,y)->(int_of_floatx,int_of_floaty))ttrinGraphics.fill_poly(Array.of_listtt);;val display_arrow : float * float -> float -> unit = <fun>
# letdisplay_label(mx,my)alab=let(sx,sy)=Graphics.text_sizelabinletpos=[float(-sx/2),float(-sy)]inletpr=rotateposainletpt=translatepr(mx,my)inletpx,py=List.hdptinletox,oy=Graphics.current_point()inGraphics.moveto((int_of_floatmx)-sx-6)((int_of_floatmy));Graphics.draw_stringlab;Graphics.movetooxoy;;val display_label : float * float -> float -> string -> unit = <fun>
# letdisplay_arcggcolij=letg=gg.rg.ginletx,y=gg.main.Upi.x,gg.main.Upi.yinifa_coutg.m.(i).(j)then(let(a1,b1)=gg.pos.(i)and(a2,b2)=gg.pos.(j)inletx0,y0=x+a1,y+b1andx1,y1=x+a2,y+b2inletrxm=(float(x1-x0))/.2.andrym=(float(y1-y0))/.2.inletxm=(floatx0)+.rxmandym=(floaty0)+.ryminGraphics.set_colorcol;Graphics.movetox0y0;Graphics.linetox1y1;leta=atan2rymrxmindisplay_arrow(xm,ym)a;display_label(xm,ym)a(string_of_float(float_of_coutg.m.(i).(j))));;val display_arc : 'a gg -> Graphics.color -> int -> int -> unit = <fun>
# letrecdisplay_shortest_pathggcoldest=letg=gg.rg.ginifappartientdestgthenletd=indexdestginletrecauxis=ifis=gg.etat.sourcethen()else(letold=gg.etat.chemins.(is)indisplay_arcggcololdis;auxold)inifnot(a_coutgg.etat.distances.(d))thenPrintf.printf"no way\n"elseauxd;;val display_shortest_path : 'a gg -> Graphics.color -> 'a -> unit = <fun>
#letdisplay_gggg()=Upi.display_rectgg.main();fori=0togg.rg.g.ind-1doforj=0togg.rg.g.ind-1doifi<>jthendisplay_arcgg(Graphics.black)ijdonedone;ifsndgg.dest!=Upi.empty_componentthendisplay_shortest_pathggGraphics.red(fstgg.dest);;val display_gg : 'a gg -> unit -> unit = <fun>
# letinverseb=letgc=Upi.get_gcbinletfcol=Upi.get_gc_fcolgcandbcol=Upi.get_gc_bcolgcinUpi.set_gc_bcolgcfcol;Upi.set_gc_fcolgcbcol;;val inverse : Upi.component -> unit = <fun>
# letaction_clicsomggbbs=let(s1,s)=gg.srcand(s2,d)=gg.destinifs==Upi.empty_componentthen(gg.src<-(som,b);inverseb)elseifd==Upi.empty_componentthen(inverseb;gg.dest<-(som,b);gg.etat<-dij_rapides1gg.rg;display_shortest_pathgg(Graphics.red)som)else(inverses;inversed;gg.dest<-(s2,Upi.empty_component);gg.src<-som,b;inverseb);;val action_clic : 'a -> 'a gg -> Upi.component -> 'b -> unit = <fun>
Les boutons sont créés automatiquement et sont bien ajoutés à la fenêtre principale.
# letmaj_gggggwghloptlopt2=letgc=Upi.make_default_context()inUpi.set_gcgclopt;(* calcul de la taille max des boutons *)letvs=Array.mapgg.to_stringgg.rg.g.sommetsinletvsize=Array.mapGraphics.text_sizevsinletw=Array.fold_right(fun(x,y)->maxx)vsize0andh=Array.fold_right(fun(x,y)->maxy)vsize0in(* création de main *)gg.main<-Upi.create_paneltruegwghlopt;gg.main.Upi.display<-display_gggg;(* et création des boutons *)letvb_bs=Array.map(funx->x,Upi.create_button(" "^(gg.to_stringx)^" ")lopt)gg.rg.g.sommetsinletf_act_b=Array.map(fun(x,(b,bs))->letac=action_clicxggbinUpi.set_bs_actionbsac)vb_bsinletbb=Array.map(function(_,(b,_))->Upi.create_borderblopt2)vb_bsinArray.iteri(funi(b)->letx,y=gg.pos.(i)inUpi.add_componentgg.mainb["PosX",Upi.Iopt(x-w/2);"PosY",Upi.Iopt(y-h/2)])bb;();;val maj_gg :'a gg ->int ->int -> (string * Upi.opt_val) list -> (string * Upi.opt_val) list -> unit =<fun>
# letidx=x;;
# letpos=[|200,300;80,200;100,100;200,100;260,200|];;
# letgg=cree_gg(create_rech_graphe(test_aho()))posidid;;
# maj_gggg400400["Background",Upi.Copt(Graphics.rgb130130130);"Foreground",Upi.CoptGraphics.green]["Relief",Upi.Sopt"Top";"Border_size",Upi.Iopt2];;
La figure 13.9 montre le chemin trouvé entre le sommet "A" et "E". Les arcs par lesquels passe le chemin changent de couleur.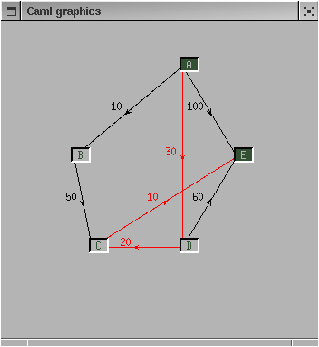
Figure 13.9 : Sélection des sommets d'une recherche
# typeg_info={spos:(int*int)array;mutableopt:Upi.lopt;mutableg_w:int;mutableg_h:int};;
# letkey2=["HAUTEUR";"LARGEUR";"POSITION";"COULEUR"];;val key2 : string list = ["HAUTEUR"; "LARGEUR"; "POSITION"; "COULEUR"]
# letlex2l=Genlex.make_lexerkey2(Stream.of_stringl);;val lex2 : string -> Genlex.token Stream.t = <fun>
# letpars2ggis=matchswithparser[<'(Genlex.Kwd"HAUTEUR");'(Genlex.Inti)>]->gi.g_h<-i|[<'(Genlex.Kwd"LARGEUR");'(Genlex.Inti)>]->gi.g_w<-i|[<'(Genlex.Kwd"POSITION");'(Genlex.Idents);'(Genlex.Inti);'(Genlex.Intj)>]->gi.spos.(indexsg)<-(i,j)|[<'(Genlex.Kwd"COULEUR");'(Genlex.Idents);'(Genlex.Intr);'(Genlex.Intg);'(Genlex.Intb)>]->gi.opt<-(s,Upi.Copt(Graphics.rgbrgb))::gi.opt|[<>]->();;val pars2 : string graphe -> g_info -> Genlex.token Stream.t -> unit = <fun>
# letcreate_gg_graphename=letg=create_graphenameinletgi={spos=Array.createg.taille(0,0);opt=[];g_w=0;g_h=0;}inletic=open_innameintryprint_string("Loading (pass 2) "^name^" : ");whiletruedoprint_string".";letl=input_lineicinpars2ggi(lex2l)done;g,giwithEnd_of_file->print_newline();close_inic;g,gi;;val create_gg_graphe : string -> string graphe * g_info = <fun>
# letcreate_appname=letg,gi=create_gg_graphenameinletsize=(string_of_intgi.g_w)^"x"^(string_of_intgi.g_h)inGraphics.open_graph(":0 "^size);letgg=cree_gg(create_rech_grapheg)gi.sposididinmaj_gggggi.g_wgi.g_h["Background",Upi.Copt(Graphics.rgb130130130);"Foreground",Upi.CoptGraphics.green]["Relief",Upi.Sopt"Top";"Border_size",Upi.Iopt2];gg;;val create_app : string -> string gg = <fun>
# letmain()=if(Array.lengthSys.argv)<>2thenPrintf.printf"Usage: dij.exe filename\n"elseletgg=create_appSys.argv.(1)inUpi.looptruefalsegg.main;;val main : unit -> unit = <fun>
ocamlc -custom -o dij.exe graphics.cma upi.cmo graphes.ml \
-cclib -lgraphics -cclib -L/usr/X11/lib -cclib -lX11
La description de la compilation d'un exécutable autonome utilisant la
bibliothèque Graphics est donnée aux chapitres 5
et 7. 

