Jeux à deux joueurs
L'application présentée dans cette section poursuit un double objectif.
D'une part elle s'attaque à une résolution de problèmes
dont la complexité empêche une exploration systématique de toutes les solutions, mettant ainsi en
valeur la bonne adéquation du langage Objective CAML pour le traitement
d'applications symboliques. D'autre part, elle permet grâce à l'utilisation
de modules paramétrés, de définir un cadre général pour la construction
de jeux à deux joueurs, permettant ainsi de factoriser une partie de
la recherche et de rendre facilement modifiable des composants comme
la fonction d'évaluation d'une position d'un jeu ou son affichage.
On présente tout d'abord la problématique des jeux à deux joueurs,
puis nous décrivons l'algorithme minimax-ab
permettant un élagage rapide de l'arbre des coups possibles. Nous
[réalisons un module paramétré implantant cet algorithme pour
décrire ensuite le module paramétré général des applications jeux
à 2 joueurs. Enfin, nous appliquons ces foncteurs pour réaliser deux
applications jeux : un puissance 4 (un morpion gravitationnel),
et Stone Henge (un jeu de construction de lignes de force).
Problématique des jeux à 2 joueurs
Les jeux à deux joueurs font partie des applications classiques en
programmation symbolique. C'est un bon exemple de résolution de problèmes
pour au moins deux raisons :
-
le nombre de solutions à analyser pour obtenir le meilleur coup
nécessite des méthodes autres que la force brute : aux échecs le
nombre de coups possibles est en moyenne de 30 et une partie se joue
en une quarantaine de coups pour chaque joueur; ce qui donne
quelques 3080 positions pour explorer l'arbre complet d'une partie!
- la qualité d'une solution est facilement vérifiable, en particulier
il est possible de tester la qualité de la solution proposée par un programme
en utilisant un autre programme.
Supposons que l'on puisse utiliser une exploration totale de toutes les parties
possibles à partir d'une position légale du jeu. Un tel programme a besoin
d'une fonction de génération des coups légaux à partir de cette position et
d'une fonction d'évaluation donnant un score à la position donnée. La
fonction d'évaluation donne un score maximal à une position gagnante et un
score minimal à une position perdante. À partir de la position initiale,
on peut donc construire l'arbre de toutes les variantes de la partie, où chaque
noeud correspond à une position, ses fils aux positions suivantes obtenues
en ayant joué un coup et les feuilles aux positions
gagnantes, perdantes ou nulles. Une fois cet arbre construit, son exploration
permet de déterminer s'il existe un chemin menant à la victoire, ou
à une position nulle le cas échéant. Le chemin de plus petite
longueur peut alors être choisi pour amener au résultat voulu.
Comme la taille d'un tel arbre est en règle générale trop grande pour
être envisageable, il est nécessaire d'en limiter sa construction. La
première possibilité est de limiter la profondeur de recherche,
c'est-à-dire le nombre de coups et de réponses à évaluer. On réduit
ainsi la profondeur de l'arbre donc sa taille. Dans ce cas on atteint
rarement des feuilles à moins d'être en fin de partie.
D'autre part, nous pouvons essayer de limiter le nombre de coups
engendrés pour pouvoir les évaluer plus finement. Pour cela, nous tentons
de n'engendrer que les coups semblant les plus favorables et de les examiner
en commençant par les meilleurs. Cela permet ainsi d'élaguer
rapidement des branches entières de l'arbre. C'est justement ce que
propose l'algorithme minimax-ab
qui est présenté dans la section suivante.
Minimax ab
On présente la recherche minimax puis on décrit sa variante optimisée
par les coupures ab. L'implantation de cet algorithme utilise un
module FAlphabeta paramétré par la représentation du jeu et
la fonction d'évaluation. On distingue les deux joueurs en les nommant A et B.
Minimax
L'algorithme minimax est un algorithme de recherche en
profondeur, avec une profondeur limitée. Il nécessite d'utiliser :
-
une fonction de génération des coups légaux à partir d'une position,
- et une fonction d'évaluation d'une position de jeu.
À partir d'une position du jeu, l'algorithme explore l'arbre de tous les coups légaux
jusqu'à la profondeur demandée. Les scores des feuilles de l'arbre sont alors calculés
par la fonction d'évaluation.
Un score positif indique une bonne position pour le joueur A, un score négatif une mauvaise
position pour le joueur A donc une bonne position pour le joueur B. Selon le joueur qui joue,
le passage d'une position à une autre est maximisante (pour le joueur A) ou minimisante
(pour le joueur B).
Les joueurs essaient de jouer les coups les plus profitables pour eux-mêmes. En
cherchant le meilleur coup pour le joueur A, la recherche en profondeur 1
cherchera à déterminer le coup immédiat qui maximise le score de la nouvelle position.
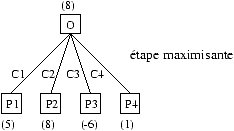
Figure 17.1 : recherche maximisante à un niveau
Sur la figure 17.1, le joueur A part de la position O,
détermine quatre coups légaux, construit ces nouvelles configurations
et les évalue. De ces scores, sa meilleur position est P2 (de score
8). Il propage cette valeur à la position O, indiquant par là que
cette position amène en un coup à une nouvelle position de score 8 en
jouant le coup C2. L'exploration en profondeur 1 est en règle
générale insuffisante, car on ne tient pas compte de la réponse de
l'adversaire. Cela produit des programmes cherchant le gain immédiat
de matériel (comme la prise d'une reine aux échecs), sans s'apercevoir
que les pièces sont protégées ou que la position devient perdante
(gambit de la reine pour faire mat). Une exploration de profondeur 2
permet de s'apercevoir du contrecoup.
La figure 17.2 montre un niveau supplémentaire de
développement de l'arbre en tenant compte de la réponse du joueur
B. Celui-ci recherche aussi son meilleur coup. Pour cela l'algorithme
minimax minimisera les scores des noeuds de profondeur 2.
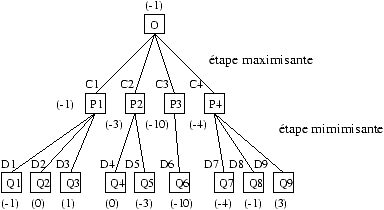
Figure 17.2 : recherche maximisante et minimisante à deux niveaux
Le coup P2 qui amenait à une position immédiate de score 8, va en fait
amener la position du jeu à un score de -3. En effet si B joue le coup
D5, alors le score de la position Q5 vaut -3. On s'aperçoit alors que
le coup C1 limite les dégats avec un score de -1. Il sera donc
préféré.
Dans la plupart des jeux, il est possible de faire lanterner son
adversaire, en le faisant jouer à coups forcés, dans le but
d'embrouiller la situation en espérant qu'il commette une faute. Pour
cela la recherche de profondeur 2 est très insuffisante pour le côté
tactique du jeu. Le côté stratégique est rarement bien exploité par un
programme car il n'a pas la vision de la probable évolution de la
position en fin de partie. La difficulté de profondeur plus grande
provient de l'explosion combinatoire. Par exemple aux échecs,
l'exploration de 2 profondeurs supplémentaires apporte un facteur
d'environ mille fois plus de combinaisons (30 * 30). Donc si on
cherche à calculer une profondeur de 10, on obtiendra environ 514
positions, ce qui est bien entendu trop. Pour cela on essaie d'élaguer
l'arbre de recherche. On peut noter que dans la figure
17.2, il n'est pas forcément utile d'explorer la branche P3
dans la mesure où le score de cette position à la profondeur 1 (voir
figure 17.1) est déjà moins bon que celui trouvé dans la
branche P1. De même la branche P4 n'a pas besoin d'être complètement
explorée. Dès le calcul de Q7, on obtient un score inférieur à celui
de P1 (toujours complètement explorée). Les calculs de Q8 et Q9 ne
pourront pas améliorer cette situation même si leur score respectif
est meilleur que Q7. Dans une étape minimisante, le score le plus
faible est remonté. On sait déjà qu'ils n'apporteront rien de nouveau.
La variante ab du minimax utilise cet élagage pour diminuer
le nombre de branches à explorer.
Minimax-ab
On appelle coupure a la borne inférieure d'un noeud
maximisant, et coupure b la borne supérieure d'un noeud
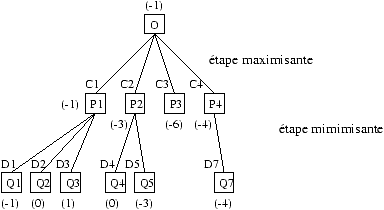
minimisant. La figure 17.3 montre les coupures
effectuées dans les branches P3 et P4 par la connaissance de la borne
inférieure -1 de P1.
Figure 17.3 : coupure a dans une étape max-min
Dès que l'arbre est plus large ou plus profond le nombre de
coupures augmente, élagant ainsi de grands sous-arbres.
Module paramétré pour le minimax-ab
On désire réaliser un module paramétré FAlphabeta qui implante cet
algorithme, réutilisable pour tout jeu à deux joueurs. Ses
paramètres correspondent d'une part à toutes les informations
d'arbitrage du jeu et d'autre part à la fonction d'évaluation.
Interfaces
On déclare les signatures REPRESENTATION, pour la
représentation du jeu, et EVAL, pour l'évaluation d'une position.
# module type REPRESENTATION = sig
type jeu
type coup
val jeu_depart : unit -> jeu
val coups_legaux: bool -> jeu -> coup list
val jouer: bool -> coup -> jeu -> jeu
end;;
# module type EVAL =
sig
type jeu
val evaluer: bool -> jeu -> int
val plusI : int
val moinsI: int
val est_feuille: bool -> jeu -> bool
val est_stable: bool -> jeu -> bool
type etat = G | P | N | C
val etat_de : bool -> jeu -> etat
end;;
Les types jeu et coup sont abstraits. Un joueur sera représenté par un booléen.
La fonction coups_legaux prend un joueur, une position et retourne la liste des
coups possibles. La fonction jouer prend un joueur, un coup,
une position et retourne une nouvelle position. Les valeurs plusI
et moinsI sont les bornes des valeurs retournées par la fonction evaluer.
Le prédicat est_feuille vérifie si un joueur dans une position donnée peut jouer.
Le prédicat est_stable indique si la position pour le joueur est dans une
situation stable. Les résultats des ces fonctions influencent la poursuite de l'exploration
de coups quand on atteint la profondeur prévue.
La signature ALPHABETA correspond à la signature résultant
de l'application totale du module paramétré que l'on
désire réaliser.
Celle-ci masque les différentes fonctions auxiliaires
que nous utiliserons pour l'implantation de l'algorithme.
# module type ALPHABETA = sig
type jeu
type coup
val alphabeta : int -> bool -> jeu -> coup
end ;;
La fonction alphabeta prend en paramètre la profondeur de la
recherche, le joueur et la position du jeu, elle retourne le coup déterminé.
On définit enfin la signature fonctionnelle
FALPHABETA que devra respecter l'implantation du foncteur.
# module type FALPHABETA =
functor (Rep : REPRESENTATION) ->
functor (Eval : EVAL with type jeu = Rep.jeu) ->
ALPHABETA with type jeu = Rep.jeu and type coup = Rep.coup ;;
Implantation
Le module paramétré FAlphabetaO explicite le partage du type jeu
entre ses deux paramètres Rep et Eval.
Ce module ne comprend que six fonctions
et deux exceptions. Le joueur true cherche à maximiser son score alors que le joueur
false le minimise. La fonction maxmin_iter calcule le maximum entre
le meilleur score des branches
à partir d'un coup du joueur true et la borne a.
La fonction maxmin prend quatre paramètres : prof qui indique
la profondeur actuelle du calcul, noeud une position du jeu, alpha et
beta les bornes des coupures. Si le noeud est une feuille de l'arbre ou si la profondeur
maximale est atteinte alors la fonction retourne l'évaluation de la position. Si ce n'est pas le cas,
elle applique à tous les coups légaux du joueur true la fonction maxmin_iter
en lui passant la fonction de poursuite de calcul dont la profondeur est décrémentée (minmax).
Cette dernière cherchera à minimiser le score de la réponse du joueur false.
Les coupures sont implantées par des exceptions.
Si la coupure b est déclenchée dans l'itération sur les coups légaux de la
fonction maxmin, alors celle-ci retourne immédiatement avec la valeur propagée
par l'exception. Les fonctions minmax_iter et minmax effectuent le travail pour l'autre joueur. La fonction cherche détermine le coup à jouer à partir du meilleur score en
parcourant les listes des scores et des coups.
La fonction principale alphabeta de ce module calcule
les coups légaux d'une position pour un joueur donné et lance les recherches à la profondeur indiquée
puis retourne le meilleur coup.
# module FAlphabetaO
(Rep : REPRESENTATION) (Eval : EVAL with type jeu = Rep.jeu) =
struct
type jeu = Rep.jeu
type coup = Rep.coup
exception AlphaCoupure of int
exception BetaCoupure of int
let maxmin_iter noeud minmax_cur beta alpha cp =
let alpha_resu =
max alpha (minmax_cur (Rep.jouer true cp noeud) beta alpha)
in if alpha_resu >= beta then raise (BetaCoupure alpha_resu)
else alpha_resu
let minmax_iter noeud maxmin_cur alpha beta cp =
let beta_resu =
min beta (maxmin_cur (Rep.jouer false cp noeud) alpha beta)
in if beta_resu <= alpha then raise (AlphaCoupure beta_resu)
else beta_resu
let rec maxmin prof noeud alpha beta =
if (prof < 1 & Eval.est_stable true noeud)
or Eval.est_feuille true noeud
then Eval.evaluer true noeud
else
try let prev = maxmin_iter noeud (minmax (prof - 1)) beta
in List.fold_left prev alpha (Rep.coups_legaux true noeud)
with BetaCoupure a -> a
and minmax prof noeud beta alpha =
if (prof < 1 & Eval.est_stable false noeud)
or Eval.est_feuille false noeud
then Eval.evaluer false noeud
else
try let prev = minmax_iter noeud (maxmin (prof - 1)) alpha
in List.fold_left prev beta (Rep.coups_legaux false noeud)
with AlphaCoupure b -> b
let rec cherche a l1 l2 = match (l1,l2) with
(h1::q1, h2::q2) -> if a = h1 then h2 else cherche a q1 q2
| ([], []) -> failwith ("AB: "^(string_of_int a)^" non trouve'")
| (_ , _) -> failwith "AB: longueur diff"
(* val alphabeta : int -> bool -> Rep.jeu -> Rep.coup *)
let alphabeta prof joueur racine =
let alpha = ref Eval.moinsI and beta = ref Eval.plusI in
let l = ref [] in
let cpl = Rep.coups_legaux joueur racine in
let eval =
try
for i = 0 to (List.length cpl) - 1 do
if joueur then
let b = Rep.jouer joueur (List.nth cpl i) racine in
let a = minmax (prof-1) b !beta !alpha
in l := a :: !l ;
alpha := max !alpha a ;
(if !alpha >= !beta then raise (BetaCoupure !alpha) )
else
let a = Rep.jouer joueur (List.nth cpl i) racine in
let b = maxmin (prof-1) a !alpha !beta
in l := b :: !l ;
beta := min !beta b ;
(if !beta <= !alpha then raise (AlphaCoupure !beta))
done ;
if joueur then !alpha else !beta
with
BetaCoupure a -> a
| AlphaCoupure b -> b
in
l := List.rev !l ;
cherche eval !l cpl
end ;;
On peut alors fermer le module FAlphabetaO en lui associant
cette signature.
# module FAlphabeta = (FAlphabetaO : FALPHABETA);;
module FAlphabeta : FALPHABETA
C'est ce dernier module qui est ensuite utilisé sur différentes
représentations et fonctions d'évaluation de jeu.
Organisation d'un programme de jeux
L'organisation d'un programme de jeu à 2 joueurs doit bien séparer
la partie spécifique à un jeu donné de la partie commune à toutes les
applications de jeux. Pour cela on se propose d'utiliser plusieurs
modules paramétrés par les modules spécifiques, permettant ainsi
d'éviter de réécrire à chaque fois les parties communes.
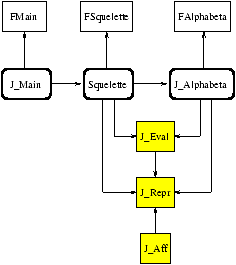
La figure 17.4 montre l'organisation choisie.
Figure 17.4 : organisation d'une application de jeux
Les modules sur fond blanc correspondent aux parties communes de
l'application. Ce sont des modules paramétrés. On y retrouve le
foncteur FAlphabeta décrit précédemment. Les modules sur fond
grisé sont les modules spécifiques au jeu. Les trois principaux sont
la représentation du jeu (J_Repr), l'affichage du jeu
(J_Aff) et la fonction d'évaluation (J_Eval). Les
modules aux bords gras arrondis sont obtenus par l'application des modules
paramétrés sur les modules simples spécifiques au jeu.
Le module FAlphabeta vient d'être décrit. Les deux autres
modules communs sont FMain qui contient la boucle principale
et FSquelette pour la gestion des joueurs.
Module FMain
Le module Fmain contient le point d'entrée de l'exécution
d'un programme de jeux. Il est paramétré par un module de signature
SQUELETTE de description de l'interaction avec un joueur dont
voici la définition.
# module type SQUELETTE = sig
val accueil: unit -> unit
val init: unit -> ((unit -> unit) * (unit -> unit))
val encore: unit -> bool
val fin: unit -> unit
exception Gagne
exception Perd
exception Nul
val gagne: unit -> unit
val perd: unit -> unit
val nul: unit -> unit
end ;;
La fonction init construit un couple des fonctions d'action de chaque joueur.
Les autres fonctions servent à gérer l'interaction d'une partie.
Le module FMain contient deux fonctions : ca_joue qui fait alterner les joueurs
et main qui gère la boucle principale.
# module FMain (P : SQUELETTE) =
struct
let ca_joue tours = while true do (fst tours) () ; (snd tours) () done
let main () = let fini = ref false
in P.accueil ();
while not !fini do
( try ca_joue (P.init ())
with P.Gagne -> P.gagne ()
| P.Perd -> P.perd ()
| P.Nul -> P.nul () );
fini := not (P.encore ())
done ;
P.fin ()
end ;;
module FMain :
functor(P : SQUELETTE) ->
sig
val ca_joue : (unit -> 'a) * (unit -> 'b) -> unit
val main : unit -> unit
end
Module FSquelette
Le module paramétré FSquelette gère les tours de chaque joueur selon
les indications fournies en début de partie
comme la nature des joueurs (programme ou non) et l'ordre des joueurs.
Il a besoin de plusieurs paramètres pour
la représentation du jeu, son affichage, sa fonction d'évaluation et la recherche ab
comme cela est décrit à la figure 17.4.
On donne d'abord la signature manquante pour l'affichage.
# module type AFFICHAGE = sig
type jeu
type coup
val accueil: unit -> unit
val fin: unit -> unit
val gagne: unit -> unit
val perd: unit -> unit
val nul: unit -> unit
val init: unit -> unit
val affiche : bool -> coup -> jeu -> jeu -> unit
val choix : bool -> jeu -> coup
val q_jouer : unit -> bool
val q_commencer : unit -> bool
val q_continuer : unit -> bool
end ;;
Il est à noter que la représentation du jeu
et celle des coups doivent être partagées par tous les modules
paramètres, d'où les contraintes sur les types. Les deux fonctions
principales sont tourH et tourM, elles gèrent
respectivement le tour d'un joueur humain (utilisant la fonction
Aff.choix) et celui d'un programme. La fonction init
détermine la nature des joueurs suite aux réponses des appels à
Aff.q_jouer
# module FSquelette
(Rep : REPRESENTATION)
(Aff : AFFICHAGE with type jeu = Rep.jeu and type coup = Rep.coup)
(Eval : EVAL with type jeu = Rep.jeu)
(Alpha : ALPHABETA with type jeu = Rep.jeu and type coup = Rep.coup) =
struct
let prof = ref 4
exception Gagne
exception Perd
exception Nul
let gagne = Aff.gagne
let perd = Aff.perd
let nul = Aff.nul
let encore = Aff.q_continuer
let le_jeu = ref (Rep.jeu_depart())
let fin = Aff.fin
let accueil = Aff.accueil
let tourH joueur () =
let choix = Aff.choix joueur !le_jeu in
let ancien_jeu = !le_jeu
in le_jeu := Rep.jouer joueur choix !le_jeu ;
Aff.affiche joueur choix ancien_jeu !le_jeu ;
match Eval.etat_de joueur !le_jeu with
Eval.P -> raise Perd
| Eval.G -> raise Gagne
| Eval.N -> raise Nul
| _ -> ()
let tourM joueur () =
let choix = Alpha.alphabeta !prof joueur !le_jeu in
let ancien_jeu = !le_jeu
in le_jeu := Rep.jouer joueur choix !le_jeu ;
Aff.affiche joueur choix ancien_jeu !le_jeu ;
match Eval.etat_de joueur !le_jeu with
Eval.G -> raise Gagne
| Eval.P -> raise Perd
| Eval.N -> raise Nul
| _ -> ()
let init () =
let a = Aff.q_jouer () in
let b = Aff.q_jouer()
in le_jeu :=Rep.jeu_depart () ;
Aff.init () ;
match (a,b) with
true,true -> tourM true, tourM false
| true,false -> tourM true, tourH false
| false,true -> tourH true, tourM false
| false,false -> tourH true, tourH false
end ;;
Les parties indépendantes du jeu sont maintenant réalisées. On
peut donc commencer la programmation de différents jeux. Cette
organisation modulaire facilite les modifications de l'affichage ou
de la fonction d'évaluation d'un jeu comme nous allons le voir.
Puissance 4
On s'intéresse tout d'abord à un premier jeu simple, un morpion
gravitationnel, appelé habituellement Puissance 4. Le jeu est
représenté par sept colonnes de six lignes.
À chaque tour un joueur pose dans une colonne un jeton de sa couleur, celui-ci
tombe jusqu'au premier emplacement libre de sa colonne. Si une colonne est complètement remplie, aucun joueur ne peut y jouer. La partie se termine quand
un des joueurs a relié une ligne de quatre pièces (horizontale,
verticale, ou diagonale), dans ce cas il a gagné,
ou quand toutes les colonnes sont pleines et dans ce cas la partie est nulle.
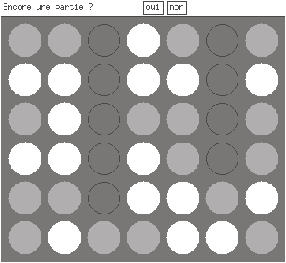
La figure 17.5 montre une partie finie.
Figure 17.5 : Une partie de Puissance 4
On remarque une ligne de quatre jetons gris en diagonale partant du coin en bas à droite.
Représentation du jeu : module P4_rep
On choisit pour ce jeu une représentation matricielle. Chaque
case de la matrice est vide ou bien contient un jeton d'un des deux
joueurs. Un coup est le numéro d'une colonne. Les coups légaux sont
les colonnes dont la dernière case n'est pas remplie.
# module P4_rep = struct
type cell = A | B | Vide
type jeu = cell array array
type coup = int
let col = 7 and lig = 6
let jeu_depart () = Array.create_matrix lig col Vide
let coups_legaux b m =
let l = ref [] in
for c = 0 to col-1 do if m.(lig-1).(c) = Vide then l := (c+1) :: !l done;
!l
let ajoute mat c =
let l = ref lig
in while !l > 0 & mat.(!l-1).(c-1) = Vide do decr l done ; !l + 1
let jouer_gen cp m e =
let mj = Array.map Array.copy m
in mj.((ajoute mj cp)-1).(cp-1) <- e ; mj
let jouer b cp m = if b then jouer_gen cp m A else jouer_gen cp m B
end ;;
On peut facilement vérifier que ce module accepte les contraintes de
la signature
REPRESENTATION.
# module P4_rep_T = (P4_rep : REPRESENTATION) ;;
module P4_rep_T : REPRESENTATION
Affichage du jeu : module P4_text
Le module P4_text décrit une interface textuelle pour le jeu Puissance 4 compatible
avec la signature AFFICHAGE. Il ne présente pas de grande difficulté, mais permet de bien
comprendre ensuite l'assemblage des modules.
# module P4_text = struct
open P4_rep
type jeu = P4_rep.jeu
type coup = P4_rep.coup
let print_jeu mat =
for l = lig - 1 downto 0 do
for c = 0 to col - 1 do
match mat.(l).(c) with
A -> print_string "X "
| B -> print_string "O "
| Vide -> print_string ". "
done;
print_newline ()
done ;
print_newline ()
let accueil () = print_string "P4 ...\n"
let fin () = print_string "A bientôt ... \n"
let question s = print_string s; print_string " o/n ? " ; read_line() = "o"
let q_commencer () = question "Voulez-vous commencer"
let q_continuer () = question "Encore une partie"
let q_jouer () = question "Est-ce une machine qui joue ?"
let gagne ()= print_string "Le 1er joueur gagne" ; print_newline ()
let perd () = print_string "Le 1er joueur perd" ; print_newline ()
let nul () = print_string "Partie nulle" ; print_newline ()
let init () = print_string "X: 1er joueur O: 2eme joueur";
print_newline () ; print_newline () ;
print_jeu (jeu_depart ()) ; print_newline()
let affiche b c aj j = print_jeu j
let est_coup = function '1'..'7' -> true | _ -> false
exception Coup of int
let rec choix joueur jeu =
print_string ("Choix joueur" ^ (if joueur then "1" else "2") ^ " : ") ;
let l = coups_legaux joueur jeu
in try while true do
let i = read_line()
in ( if (String.length i > 0) && (est_coup i.[0])
then let c = (int_of_char i.[0]) - (int_of_char '0')
in if List.mem c l then raise (Coup c) );
print_string "coup non valable, essayez encore : "
done ;
List.hd l
with Coup i -> i
| _ -> List.hd l
end ;;
On vérifie immédiatement qu'il respecte bien les contraintes de la signature AFFICHAGE.
# module P4_text_T = (P4_text : AFFICHAGE) ;;
module P4_text_T : AFFICHAGE
Fonction d'évaluation : module P4_eval
La qualité d'un jeu dépend
principalement de la fonction d'évaluation d'une position. Le module P4_eval définit
la fonction evaluer qui calcule la valeur d'une position pour un joueur donné. Cette fonction
appelle la fonction eval_bloc, dans les quatre directions en spécialisant
les diagonales, qui elle-même appelle la fonction eval_quatre pour calculer le nombre de
jetons dans la ligne demandée.
Le tableau valeur donne la valeur d'un bloc contenant 0, 1, 2
ou 3 jetons de la même couleur. L'exception Quatre est
déclenchée quand 4 jetons sont alignés.
# module P4_eval = struct
open P4_rep
type jeu = P4_rep.jeu
let valeur = Array.of_list [0; 2; 10; 50]
exception Quatre of int
exception Valeur_nulle
exception Arg_invalid
let moinsI = -10000
let plusI = 10000
let eval_quatre m l_dep c_dep delta_l delta_c =
let n = ref 0 and e = ref Vide
and x = ref c_dep and y = ref l_dep
in try
for i = 1 to 4 do
if !y<0 or !y>=lig or !x<0 or !x>=col then raise Arg_invalid ;
( match m.(!y).(!x) with
A -> if !e = B then raise Valeur_nulle ;
incr n ;
if !n = 4 then raise (Quatre plusI) ;
e := A
| B -> if !e = A then raise Valeur_nulle ;
incr n ;
if !n = 4 then raise (Quatre moinsI);
e := B;
| Vide -> () ) ;
x := !x + delta_c ;
y := !y + delta_l
done ;
valeur.(!n) * (if !e=A then 1 else -1)
with
Valeur_nulle | Arg_invalid -> 0
let eval_bloc m e cmin cmax lmin lmax dx dy =
for c=cmin to cmax do for l=lmin to lmax do
e := !e + eval_quatre m l c dx dy
done done
let evaluer b m =
try let evaluation = ref 0
in (* evaluation des lignes *)
eval_bloc m evaluation 0 (lig-1) 0 (col-4) 0 1 ;
(* evaluation des colonnes *)
eval_bloc m evaluation 0 (col-1) 0 (lig-4) 1 0 ;
(* diagonales partant de la premiere ligne (à droite) *)
eval_bloc m evaluation 0 (col-4) 0 (lig-4) 1 1 ;
(* diagonales partant de la premiere colonne (à droite) *)
eval_bloc m evaluation 1 (lig-4) 0 (col-4) 1 1 ;
(* diagonales partant de la premiere ligne (à gauche) *)
eval_bloc m evaluation 3 (col-1) 0 (lig-4) 1 (-1) ;
(* diagonales partant de la derniere colonne (à gauche) *)
eval_bloc m evaluation 1 (lig-4) 3 (col-1) 1 (-1) ;
!evaluation
with Quatre v -> v
let est_feuille b m = let v = evaluer b m
in v=plusI or v=moinsI or coups_legaux b m = []
let est_stable b j = true
type etat = G | P | N | C
let etat_de joueur m =
let v = evaluer joueur m
in if v = plusI then if joueur then G else P
else if v = moinsI then if joueur then P else G
else if coups_legaux joueur m = [] then N else C
end ;;
Le module P4_eval est compatible avec les contraintes de la signature EVAL
# module P4_eval_T = (P4_eval : EVAL) ;;
module P4_eval_T : EVAL
Pour faire jouer deux fonctions d'évaluation l'une contre l'autre, il
faut modifier la fonction evaluer
en aiguillant chaque joueur sur sa fonction d'évaluation propre.
Assemblage des modules
Toutes les briques nécessaires à la réalisation du jeu puissance 4 sont maintenant réalisées.
Il ne reste plus qu'à les assembler selon le schéma de la figure
17.4.
On construit tout d'abord le squelette P4_Squelette qui est l'application du module paramétré FSquelette
aux modules P4_rep, P4_text, P4_eval et au résultat de l'application du module
paramétré FAlphabeta sur P4_rep et P4_eval.
# module P4_squelette =
FSquelette (P4_rep) (P4_text) (P4_eval) (FAlphabeta (P4_rep) (P4_eval)) ;;
module P4_squelette :
sig
val prof : int ref
exception Gagne
exception Perd
exception Nul
val gagne : unit -> unit
val perd : unit -> unit
val nul : unit -> unit
val encore : unit -> bool
val le_jeu : P4_text.jeu ref
val fin : unit -> unit
val accueil : unit -> unit
val tourH : bool -> unit -> unit
val tourM : bool -> unit -> unit
val init : unit -> (unit -> unit) * (unit -> unit)
end
On obtient alors le module principal P4_main de l'application du module paramétré FMain sur
le résultat de l'application précédente P4_squelette.
# module P4_main = FMain(P4_squelette) ;;
module P4_main :
sig
val ca_joue : (unit -> 'a) * (unit -> 'b) -> unit
val main : unit -> unit
end
Le lancement du jeu s'effectue par l'application de la fonction P4_main.main sur ().
Test du jeu
Tel que le squelette général des jeux a été écrit, il est possible
de faire jouer deux personnes entre elles (le programme ne sert que d'arbitre), une personne contre le programme
ou le programme contre lui-même. Bien que cette dernière possibilité ne présente que peu d'intérêt pour un joueur,
elle permet de lancer des tests plus facilement sans devoir attendre la réponse d'un joueur.
Le jeu suivant choisit cette option.
# P4_main.main ();;
P4 ...
Est-ce une machine qui joue ? o/n ? o
Est-ce une machine qui joue ? o/n ? o
X: 1er joueur O: 2eme joueur
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
Une fois la position initiale affichée, le joueur 1 (joué par le programme) calcule
son coup qui est ensuite affiché.
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . X .
Le joueur 2 (toujours joué par le programme) calcule son propre coup et le jeu s'affiche.
Le jeu se poursuit ainsi de suite jusqu'à une position de fin de partie. Dans le cas présent le joueur 1 gagne la partie sur la position finale suivante :
. O O O . O .
. X X X . X .
X O O X . O .
X X X O . X .
X O O X X O .
X O O O X X O
Le 1er joueur gagne
Encore une partie o/n ? n
A bientot ...
- : unit = ()
Interface graphique
Comme le plaisir de jouer provient aussi de l'interface graphique du
programme, on définit un nouveau module P4_graph compatible
avec la signature AFFICHAGE qui ouvre une
fenêtre graphique et gère les clics souris. On retrouve le texte de ce module dans le sous-catalogue
Applications du CD-ROM (voir page ??).
On crée alors un nouveau squelette (P4_squeletteG) qui
résulte de l'application du module paramétré FSquelette.
# module P4_squeletteG =
FSquelette (P4_rep) (P4_graph) (P4_eval) (FAlphabeta (P4_rep) (P4_eval)) ;;
Seul le paramètre du module d'affichage diffère de la version texte
dans l'application du module paramétré FSquelette. On crée
alors le module principal de l'application Puissance 4 avec interface
graphique.
# module P4_mainG = FMain(P4_squeletteG) ;;
module P4_mainG :
sig
val ca_joue : (unit -> 'a) * (unit -> 'b) -> unit
val main : unit -> unit
end
L'évaluation de l'expression P4.mainG.main() affiche la
fenêtre graphique de la figure 17.5 et gère l'interaction
avec le joueur.
Stone Henge
Le jeu Stone Henge, dû à Reiner Knizia, est un jeu de construction de lignes de force.
Les règles sont simples à apprendre, mais l'intérêt du jeu reste grand même après
de nombreuses parties. La règle en ligne peut être consultée au lien suivant :
Lien
http://www.gamecabinet.com/frenchRules/Stonehenge.html
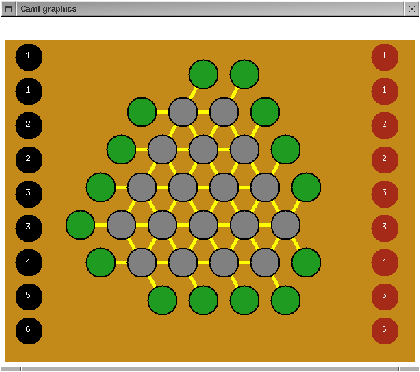
La position initiale du jeu est représentée à la figure 17.6.
Présentation du jeu
Le but du jeu est de gagner au moins 8 lignes de force (lignes claires) sur les 15 existantes. Le
gain d'une ligne est visualisé par la pose d'un menhir (ou mégalithe) sur une case gris foncé associée à une ligne de force.
Figure 17.6 : Position initiale de Stone Henge
À son tour chaque joueur pose une pierre (sur les 9 qu'il possède au début) numérotée (de 1 à 6)
sur une des 18 cases centrales grises. On ne peut pas poser une pierre sur une case occupée.
Une fois une pierre posée, une ou plusieurs lignes de force peuvent être perdues ou gagnées.
Une
ligne de force est gagnée par un joueur si l'autre joueur ne peut pas dépasser le
score (total des pierres déjà posées d'une couleur)
du premier, même en remplissant les cases encore vides de cette ligne par ses meilleures pierres.
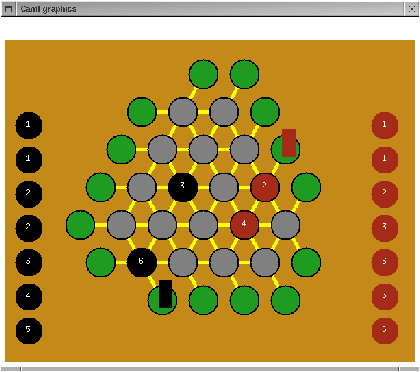
Par exemple, à la figure 17.7, le joueur noir commence par poser la pierre de valeur 3,
le joueur rouge sa pierre 2, puis le joueur noir joue sa pierre 6 et gagne une ligne. Le joueur rouge
pose alors sa pierre 4 et gagne aussi une ligne de force. Celle-ci
n'est pas encore complètement remplie, mais le joueur noir ne pourra
jamais dépasser le score de son adversaire.
On peut noter que le joueur rouge aurait pu jouer une pierre 3 à la place de sa pierre 4. En effet il reste une seule case libre sur cette ligne de force et la pierre la plus forte de noir vaut 5, donc noir
ne peut plus battre rouge sur cette ligne.
Figure 17.7 : Position après 4 coups
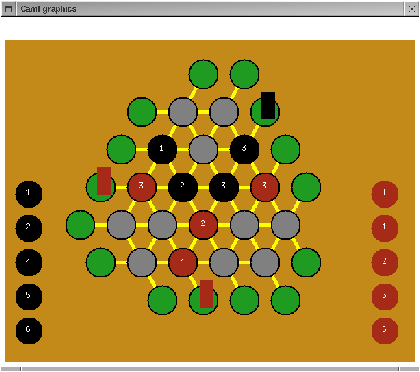
Dans un cas d'égalité sur une ligne pleine, celui qui a posé la dernière pierre et qui n'a pas pu battre le score de son adversaire perd cette ligne. La figure 17.8 montre un tel cas.
Le dernier coup de rouge est la pierre 4. Sur la ligne pleine où le 4 est posé il y a égalité. Comme rouge est le dernier joueur a y avoir posé une pierre, il n'a pas pu battre son adversaire et perd la ligne,
d'où le menhir noir qui indique le gain de noir. On s'aperçoit que la fonction jouer qui effectue
le rôle d'arbitre doit tenir compte de ces subtilités de pose de menhirs.
Figure 17.8 : Position après 6 coups
Il n'y a jamais de partie nulle à ce jeu. Il y a 15 lignes et toutes sont prises à un moment de la partie,
donc un des deux joueurs atteint le gain d'au moins 8 lignes.
Complexité de la recherche
Avant toute implantation d'un nouveau jeu, il est nécessaire de calculer le
nombre de coups légaux
entre deux tours de jeu ainsi que le nombre de coups d'une partie.
On détermine alors la profondeur raisonnable de l'algorithme minimax-ab.
Dans le jeu StoneHenge le nombre de coups
d'une partie est borné par le nombre de jetons des deux joueurs, c'est-à-dire 18. Le nombre de coups possibles
diminue au fur et à mesure de la partie. Au premier coup de la partie, le
joueur a 6 jetons différents et 18 cases libres, ce qui lui fait 108 coups légaux. Au deuxième coup,
le deuxième joueur a aussi 6 jetons différents pour 17 cases libre (102 coups légaux). Le fait de passer d'une profondeur
de 2 à 4 pour les premiers coups de la partie fait passer d'environ 104 coups à 108 coups.
Par contre en fin de partie, disons sur les 8 derniers coups, la complexité se réduit fortement.
Si on calcule le pire des cas (tous les jetons sont différents) on obtient environ 23 millions de possibilités :
4*8 * 4*7 * 3*6 * 3*5 * 2*4 * 2*3 * 1*2 * 1*1 = 23224320
Il semble délicat de calculer au delà d'une profondeur 2 pour les premiers coups.
Cela dépend de la fonction d'évaluation, et de sa capacité à évaluer les positions de début de partie, du moins
tant qu'il y a peu de menhirs posés.
Par contre en fin de partie la profondeur peut augmenter à 4 ou 6, mais cela
est probablement trop tard pour récupérer une position affaiblie.
Implantation
La réalisation de ce jeu suit l'organisation utilisée pour le jeu Puissance 4 et décrite à la
figure 17.4. Les deux principales
difficultés viennent du respect des règles du jeu pour la pose des menhirs et de la fonction d'évaluation qui doit pouvoir évaluer une situation le plus rapidement possible tout en étant pertinente.
On décrit tout d'abord la représentation du jeu et l'arbitre de jeu, pour s'intéresser par la suite à la fonction d'évaluation.
Représentation du jeu
Il y a quatre données particulières pour ce jeu :
-
les pierres (ou jetons) des joueurs (type pierre)
- les menhirs (type menhir)
- les 15 lignes de force
- les 18 cases où poser les pierres
On donne un numéro unique à chaque case.
1---2
/ \ / \
3---4---5
/ \ / \ / \
6---7---8---9
/ \ / \ / \ / \
10--11--12--13--14
\ / \ / \ / \ /
15--16--17--18
Par chaque case passe 3 lignes de force. On numérote aussi chaque ligne de force.
Cette description se retrouve dans la déclaration de la liste lignes, que l'on convertit
en vecteur (vecteur_l). Une case est soit vide, soit contient la pierre posée et son propriétaire.
On conserve d'autre part pour chaque case le numéro des lignes qui y passent.
Ce tableau est calculé par la fonction
lignes_par_case et est nommé num_ligne_par_case.
Le jeu est représenté par le vecteur des 18 cases, le vecteur des 15 lignes de force contenant ou non un menhir,
et des listes de jetons pour les deux joueurs. La fonction jeu_depart crée ces quatre
éléments.
Le calcul des coups légaux pour un joueur revient à un produit cartésien des jetons restants avec les cases libres.
Plusieurs fonctions utilitaires permettent de compter le score d'un joueur dans une ligne, de calculer
le nombre de cases libres d'une ligne et de vérifier si une ligne a déjà un menhir. Il ne reste plus qu'à écrire
la fonction jouer qui joue un coup et décide des menhirs à poser. Nous la décrivons à la fin du
listing suivant du module Stone_rep.
# module Stone_rep = struct
type joueur = bool
type pierre = P of int
let int_of_pierre = function P x -> x
type menhir = Rien | M of joueur
type case = Vide | Occup of joueur*pierre
let value_on_case = function
Vide -> 0
| Occup (j, x) -> int_of_pierre x
type jeu = J of case array * menhir array * pierre list * pierre list
type coup = int * pierre
let lignes = [
[0;1]; [2;3;4]; [5; 6; 7; 8;]; [9; 10; 11; 12; 13]; [14; 15; 16; 17];
[0; 2; 5; 9]; [1; 3; 6; 10; 14]; [4; 7; 11; 15]; [8; 12; 16]; [13; 17];
[9; 14]; [5; 10; 15]; [2; 6; 11; 16]; [0; 3; 7; 12; 17]; [1; 4; 8; 13] ]
let vecteur_l = Array.of_list lignes
let lignes_par_case v =
let t = Array.length v in
let r = Array.create 18 [||] in
for i = 0 to 17 do
let w = Array.create 3 0
and p = ref 0 in
for j=0 to t-1 do if List.mem i v.(j) then (w.(!p) <- j; incr p)
done;
r.(i) <- w
done;
r
let num_ligne_par_case = lignes_par_case vecteur_l
let rec lignes_de_i i l = List.filter (fun t -> List.mem i t) l
let lignes_des_cases l =
let a = Array.create 18 l in
for i=0 to 17 do
a.(i) <- (lignes_de_i i l)
done; a
let ldc = lignes_des_cases lignes
let jeu_depart ()= let lp = [6; 5; 4; 3; 3; 2; 2; 1; 1] in
J ( Array.create 18 Vide, Array.create 15 Rien,
List.map (fun x -> P x) lp, List.map (fun x -> P x) lp )
let rec unicite l = match l with
[] -> []
| h::t -> if List.mem h t then unicite t else h:: (unicite t)
let coups_legaux joueur (J (ca, m, r1, r2)) =
let r = if joueur then r1 else r2 in
if r = [] then []
else
let l = ref [] in
for i = 0 to 17 do
if value_on_case ca.(i) = 0 then l:= i:: !l
done;
let l2 = List.map (fun x->
List.map (fun y-> x,y) (List.rev(unicite r)) ) !l in
List.flatten l2
let copie_plateau p = Array.copy p
let copie_carnac m = Array.copy m
let rec joue_pierre caillou l = match l with
[] -> []
| x::q -> if x=caillou then q
else x::(joue_pierre caillou q)
let compte_case joueur case = match case with
Vide -> 0
| Occup (j,p) -> if j = joueur then (int_of_pierre p) else 0
let compte_ligne joueur ligne pos =
List.fold_left (fun x y -> x + compte_case joueur pos.(y)) 0 ligne
let rec compte_max n = function
[] -> 0
| t::q ->
if (n>0) then
(int_of_pierre t) + compte_max (n-1) q
else
0
let rec nbr_cases_libres ca l = match l with
[] -> 0
| t::q -> let c = ca.(t) in
match c with
Vide -> 1 + nbr_cases_libres ca q
|_ -> nbr_cases_libres ca q
let a_menhir i ma =
match ma.(i) with
Rien -> false
| _ -> true
let quel_menhir i ma =
match ma.(i) with
Rien -> failwith "quel_menhir"
| M j -> j
let est_pleine l ca = nbr_cases_libres ca l = 0
(* fonction jouer : arbitre du jeu *)
let jouer joueur coup jeu =
let (c, i) = coup in
let J (p, m, r1, r2) = jeu in
let nr1,nr2 = if joueur then joue_pierre i r1,r2
else r1, joue_pierre i r2 in
let np = copie_plateau p in
let nm = copie_carnac m in
np.(c)<-Occup(joueur,i); (* on joue le coup *)
let lignes_de_la_case = num_ligne_par_case.(c) in
(* calcul des menhirs des 3 lignes de la case *)
for k=0 to 2 do
let l = lignes_de_la_case.(k) in
if not (a_menhir l nm) then (
if est_pleine vecteur_l.(l) np then (
let c1 = compte_ligne joueur vecteur_l.(l) np
and c2 = compte_ligne (not joueur) vecteur_l.(l) np in
if (c1 > c2) then nm.(l) <- M joueur
else ( if c2 > c1 then nm.(l) <- M (not joueur)
else nm.(l) <- M (not joueur ))))
done;
(* calcul des autres menhirs *)
for k=0 to 14 do
if not (a_menhir k nm ) then
if est_pleine vecteur_l.(k) np then failwith "joueur"
else
let c1 = compte_ligne joueur vecteur_l.(k) np
and c2 = compte_ligne (not joueur) vecteur_l.(k) np in
let cases_libres = nbr_cases_libres np vecteur_l.(k) in
let max1 = compte_max cases_libres
(if joueur then nr1 else nr2)
and max2 = compte_max cases_libres
(if joueur then nr2 else nr1) in
if c1 >= c2 + max2 then nm.(k) <- M joueur
else if c2 >= c1 + max1 then nm.(k) <- M (not joueur)
done;
J(np,nm,nr1,nr2)
end;;
La fonction jouer se découpe en 3 étapes :
-
la recopie du jeu et la pose du coup;
- la détermination de la pose d'un menhir sur une des trois lignes de la case jouée;
- le traitement des autres lignes de force.
La deuxième étape vérifie pour chacune des 3 lignes qui passent
par cette case si elle n'a pas
déjà un menhir, puis si elle est pleine. Dans ce cas elle fait le compte pour chaque
joueur et détermine lequel est le plus grand strictement et attribue le menhir à ce joueur là. En
cas d'égalité, la ligne va au joueur adverse de celui qui vient de jouer. En effet, il n'existe pas
de ligne avec une seule case. Une ligne pleine a au moins deux pierres. Donc le joueur qui vient
de jouer a juste égalisé le score de son adversaire. Il ne peut pas prétendre gagner cette ligne qui va à son adversaire. Si la ligne traitée n'est pas pleine, elle sera analysée par l'étape 3.
La troisième étape vérifie pour chaque ligne non encore attribuée, ce qui indique par là
que la ligne n'est pas pleine, si un joueur ne peut plus être battu par son adversaire.
Dans ce cas, la ligne lui est immédiatement donnée. Pour réaliser ce test, il est nécessaire
de calculer le score maximal potentiel d'un joueur sur une ligne
(c'est à dire en utilisant ses meilleurs pierres). Si la ligne est encore en discussion rien ne se passe.
Évaluation
La fonction d'évaluation doit rester simple devant le nombre de cas à traiter
en début de jeu. L'idée est de ne pas trop simplifier le jeu en jouant immédiatement ses
pierres les plus fortes, ce qui laisserait le champ libre à l'adversaire.
Deux critères sont utilisés : le nombre de menhirs gagnés et la potentialité
des futurs coups en calculant la valeur des pierres restantes. On utilise la formule
suivante pour le joueur 1 :
score = 50 * (c1 - c2) + 10 * (pr1 - pr2)
où ci est le nombre de menhirs et pri la somme des pierres restantes du joueur i.
La formule retourne un résultat positif si les différences des menhirs (c1 - c2)
et des potentialités (pr1 - pr2) sont à l'avantage du joueur 1.
On s'aperçoit alors que la pose de la pierre 6 n'est effectuée que si elle rapporte au moins deux lignes.
Le gain d'une ligne donne 50, mais le fait de jouer 6 fait perdre 10*6 points, on préfère alors jouer 1 qui calcule le même score (perte de 10 points).
# module Stone_eval = struct
open Stone_rep
type jeu = Stone_rep.jeu
exception Fini of bool
let plusI = 1000 and moinsI = -1000
let nbr_lignes_gagnees (J(ca, m,r1,r2)) =
let c1,c2 = ref 0,ref 0 in
for i=0 to 14 do
if a_menhir i m then if quel_menhir i m then incr c1 else incr c2
done;
!c1,!c2
let rec nbr_points_restant lig = match lig with
[] -> 0
| t::q -> (int_of_pierre t) + nbr_points_restant q
let evaluer joueur jeu =
let (J (ca,ma,r1,r2)) = jeu in
let c1,c2 = nbr_lignes_gagnees jeu in
let pr1,pr2 = nbr_points_restant r1, nbr_points_restant r2 in
match joueur with
true -> if c1 > 7 then plusI else 50 * (c1 - c2) + 10 * (pr1 - pr2)
| false -> if c2 > 7 then moinsI else 50 * (c1 - c2) + 10 * (pr1 - pr2)
let est_feuille joueur jeu =
let v = evaluer joueur jeu in
v = plusI or v = moinsI or coups_legaux joueur jeu = []
let est_stable joueur jeu = true
type etat = G | P | N | C
let etat_de joueur m =
let v = evaluer joueur m in
if v = plusI then if joueur then G else P
else
if v = moinsI
then if joueur then P else G
else
if coups_legaux joueur m = [] then N else C
end;;
Assemblage
On écrit par ailleurs le module Stone_graph qui décrit une
interface graphique compatible avec la signature AFFICHAGE.
On construit Stone_squeletteG à la manière
de P4_squeletteG en passant les arguments propres au jeu Stone Henge
à l'application du module paramètre FSquelette.
# module Stone_squeletteG = FSquelette (Stone_rep)
(Stone_graph)
(Stone_eval)
(FAlphabeta (Stone_rep) (Stone_eval)) ;;
module Stone_squeletteG :
sig
val prof : int ref
exception Gagne
exception Perd
exception Nul
val gagne : unit -> unit
val perd : unit -> unit
val nul : unit -> unit
val encore : unit -> bool
val le_jeu : Stone_graph.jeu ref
val fin : unit -> unit
val accueil : unit -> unit
val tourH : bool -> unit -> unit
val tourM : bool -> unit -> unit
val init : unit -> (unit -> unit) * (unit -> unit)
end
On construit alors le module principal Stone_mainG.
# module Stone_mainG = FMain(Stone_squeletteG);;
module Stone_mainG :
sig
val ca_joue : (unit -> 'a) * (unit -> 'b) -> unit
val main : unit -> unit
end
Le lancement de Stone_mainG.main () ouvre la fenêtre de la figure 17.6. Après
le dialogue pour savoir qui joue,
la partie commence. Un joueur humain sélectionne d'abord la pierre à jouer
puis la case où la poser.
Pour en faire plus
L'organisation de ces applications utilisant plusieurs modules paramétrés permet de réutiliser pleinement
le module FAlphabeta et le module FSquelette pour les deux jeux que nous avons décrits. Néanmoins
pour le jeu Stone Henge certaines fonctions du module Stone_rep, nécessaires
pour la fonction jouer, qui n'apparaissent
pas dans la signature REPRESENTATION ont été utilisées par la fonction d'évaluation. C'est pour cela
que le module Stone_rep n'a pas été immédiatement fermé par la signature REPRESENTATION.
Cette ouverture entre modules pour la partie spécifique des jeux permet un développement plus incrémentiel
sans fragiliser le schéma de dépendances des modules présenté à la figure 17.4.
Une première amélioration concerne les jeux où d'une position et d'un coup il est facile de déterminer la position
précédente. Dans ces cas là, il peut être plus efficace de ne pas effectuer une copie du jeu par la fonction jouer, mais de conserver un historique des coups joués pour pouvoir revenir en arrière (backtraking). C'est le cas
de Puissance 4 mais pas de Stone Henge.
Une deuxième amélioration est de profiter du temps d'attente de la réponse d'un joueur pour commencer l'évaluation
des futures positions.
Pour cela on peut utiliser des processus légers (voir chapitre 19) qui
lancent le calcul pendant cette attente. Si la réponse fait partie du début de l'exploration des positions, alors le gain de temps est immédiat, sinon on repart avec la nouvelle position.
Une troisième amélioration est de constituer et d'exploiter des
bibliothèques d'ouvertures. Nous avons pu constater avec Stone
Henge, mais c'est aussi le cas pour beaucoup d'autres jeux, que l'éventail
des possibilités et donc le nombre des coups légaux à explorer
est plus important en début de partie. Il y a donc tout à gagner
à précalculer les meilleurs coups des positions de départ et à les
sauver dans un fichier. On peut enrichir l'intérêt du jeu, en faisant
intervenir le hasard pour choisir parmi un certain nombre de variantes
menant à des positions dont les valeurs sont proches.
Une quatrième voie est de ne pas borner la profondeur de la
recherche par une valeur fixe, mais par un temps de calcul à ne pas
dépasser. De la sorte, le programme devient plus efficace en fin de
partie quand l'éventail des choix se retrouve limité. Cette
modification demande de modifier quelque peu l'implantation de
minmax afin de pouvoir reprendre un arbre pour augmenter sa
profondeur. Une heuristique dépendant du jeu, donc paramètre de
minmax pourrait choisir quelles sont les branches dont
l'exploration doit être poussée et quelles sont celles qui
peuvent être abandonnées.
Il existe d'autre part de nombreux autres jeux qui ne demandent qu'à être implantés ou réimplantés.
On peut citer plusieurs classiques : Dames, Othello, Abalone, ...,
mais aussi de nombreux jeux moins connus et
néanmoins fort jouables. On trouve au lien suivant quelques projets d'étudiants
comme le jeu de Dames ou le jeu Nuba.
Lien
http://www.pps.jussieu.fr/~emmanuel/Public/enseignement/
Les jeux avec tirage aléatoire (pioche des jeux de cartes, lancement de dés)
nécessitent une modification de l'algorithme minimax-ab
pour tenir compte de la probabilité de ce tirage.
Nous reviendrons sur les interfaces des jeux au chapitre
21 en construisant des interfaces pour les
navigateurs WWW apportant sans frais la fonction retour au dernier
coup. On appréciera d'autant plus l'organisation par module, qui
permet de ne modifier qu'un élément, ici l'affichage et l'interaction,
d'une application de jeux à 2 joueurs.