La récursion sur les entiers naturels consiste à transformer un problème sur un entier naturel n en un (ou plusieurs) problèmes sur des nombres plus petits. Comme il n'existe pas de chaîne infiniment décroissante dans l'ensemble des entiers naturels, la récursion finit par atteindre des cas de base comme 0 ou 1 ou ... pour lesquels, une solution directe au problème est fournie.
 
L'ensemble des entiers naturels est dit « bien fondé » car il n'existe pas de chaîne infiniment décroissante. Cette propriété assure la récursion sur des ensembles plus complexes comme les listes ou les arbres. Prenons par exemple l'exemple de l'hydre de Lerne qu'Hercule doit vaincre. Cette hydre possède des cous portant des cous ou des têtes. Lorsqu'Hercule coupe un cou, neuf fois plus de têtes repoussent au-dessous du cou tranché comme le montre la figure ?? sauf si le cou était directement attaché à la bête.

---

---

Hercule finira donc malgré l'énorme accroissement de têtes à trancher par vaincre la bête. Le raisonnement est que la hauteur de l'arbre ne peut que décroître et quand elle ne décroit pas le nombre de cous à hauteur maximale décroit.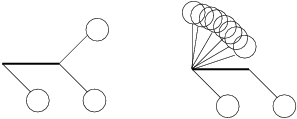
 
Si les entiers naturels forment un domaine bien fondé, ce n'est pas le cas des entiers puisqu'il existe des chaînes infiniment décroissantes telle 2, 1, 0, -1, -2, -3, ... En revanche, il est possible de projeter les entiers sur les entiers naturels et ainsi travailler avec des entiers bien fondés. Il suffit d'assimiler tous les entiers négatifs à l'entier naturel zéro. Ceci mène au concept de programmation robuste.
 
Prenons le cas de la factorielle qui s'écrit:
 

Si l'on veut adapter cette définition à tous les entiers, on pourra, par exemple, écrire:
 

Notez le changement de type: la factorielle accepte des nombres quelconques et non plus seulement des entiers naturels. Sa définition est robuste en ce sens qu'elle ne boucle jamais quelque soit la valeur de son argument (essayez par exemple (factorielle -3) ou (factorielle 3.14)) en revanche elle ne renvoie pas forcément des résultats sensés en dehors de son véritable domaine de définition.
 
En définitive, lorsque cela ne coûte rien, préférez systématiquement la robustesse. Écrivez donc plutôt ceci, à la place de la première définition plus haut, de même signature mais de définition robuste.