Barrière d'abstraction des environnements
État des lieux
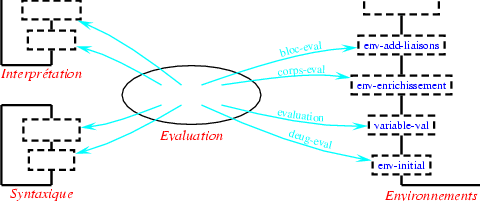
Avant d'étudier la barrière d'abstraction des environnements, nous voudrions schématiser la structure de l'évaluateur (en oubliant les fonctions de service). Nous voulions donc écrire un évaluateur:
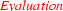
en sachant, dès le départ, qu'il faudrait une barrière syntaxique, que nous avons définie en premier, une barrière d'interprétation que nous venons de définir, et une barrière des environnements:
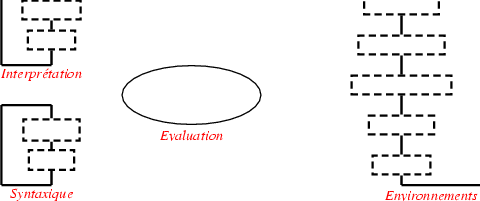
Après avoir défini la barrière syntaxique, nous avons défini la fonction deug-eval en utilisant la fonction evaluation et la fonction -- de la barrière des environnements -- env-initial:
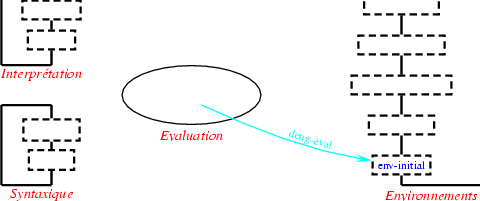
La définition de la fonction evaluation utilise les fonctions de la barrière d'abstraction, des évaluateurs spécialisés, la fonction -- de la barrière d'interprétation -- citation-val et la fonction -- de la barrière des environnements -- variable-val:
En écrivant les différents évaluateurs spécialisés, nous avons utilisé des fonctions de la barrière syntaxique et de la barrière d'interprétation ainsi que les fonctions suivantes de la barrière d'abstraction des environnements:
- la fonction env-add-liaisons lors de l'écriture de la fonction bloc-eval,
- la fonction env-enrichissement lors de l'écriture de la fonction corps-eval:
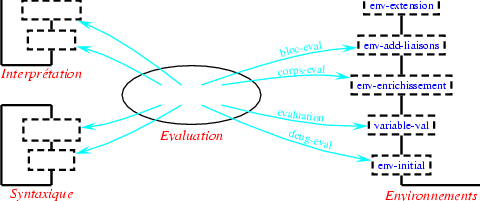
Enfin, lorsque nous avons implanté la barrière d'interprétation, en écrivant la définition de la fonction fonction-invocation, nous avons utilisé la fonction env-extension de la barrière d'abstraction des environnements:
Notion de bloc d'activation
Considérons l'« exemple » suivant:
(let ((v1 exp1)
(v2 exp2))
(define (f1 x1 x2 x3)
corps-f1)
(define (f2 y1)
corps-f2)
exp-bloc)
(v2 exp2))
(define (f1 x1 x2 x3)
corps-f1)
(define (f2 y1)
corps-f2)
exp-bloc)
a) Liaisons: ce bloc commence par des liaisons et nous devons étendre l'environnement courant en ajoutant deux associations variable -- valeur.
b) Définitions fonctionnelles: nous avons ensuite deux définitions fonctionnelles et nous devons enrichir l'environnement avec deux associations variable -- valeur fonctionnelle.
c) Application de fonction: enfin, dans exp-bloc, lors de l'application de f1 (resp. f2), nous devons évaluer corps-f1 (resp. corps-f2) dans l'environnement obtenu en étendant l'environnement mémorisé en liant les trois (resp. une) variables aux valeurs des trois (resp. un) arguments.
Ainsi, dans toutes ces étapes, nous devons ajouter à l'environnement courant un ensemble de couples d'associations variable -- valeur: nous nommerons bloc d'activation un tel ensemble (noter que cette terminologie, classique en informatique, est due à l'implantation des fonctions).
Spécification de la barrière des environnements
Rappelons tout d'abord les spécifications des fonctions sur les environnements que nous avons utilisées, en commençant par deux fonctions qui vont de soi:
| 624 |
;;; env-initial: -> Environnement
;;; (env-initial) rend l'environnement initial, i.e. l'environnement qui ;;; contient toutes les primitives. |
| 480 |
;;; variable-val: Variable * Environnement -> Valeur
;;; (variable-val var env) rend la valeur de la variable «var» dans ;;; l'environnement «env». |
Précision
Considérons la définition suivante que nous avons déjà vue en cours (la fonction rend la liste obtenue en ajoutant l'élément donné à la fin de la liste donnée), définition où nous avions globalisé une variable:
(define (&d L x)
(define (&d-x L)
(if (pair? L)
(cons (car L)
(&d-x (cdr L)))
(list x))) ; fin &d-x
(&d-x L)) ; fin &d
(define (&d-x L)
(if (pair? L)
(cons (car L)
(&d-x (cdr L)))
(list x))) ; fin &d-x
(&d-x L)) ; fin &d
Dans cette définition, de quels blocs d'activation sont extraits les valeurs des différentes occurrences des variables?
- la valeur de L de la dernière ligne doit être trouvée dans le bloc d'activation créé par la fonction sous-jacente liée à &d (la fonction externe),
- la valeur de L des lignes 3, 4 et 5 doit être trouvée dans le bloc d'activation, ou plus exactement dans le dernier bloc d'activation (récursivité), créé par la fonction sous-jacente liée à &d-x (la fonction interne),
- la valeur de x de l'avant dernière ligne devrait, de même, être trouvée dans le bloc d'activation créé par la fonction sous-jacente liée à &d-x (la fonction interne), mais, comme cette variable n'est pas présente dans ce bloc d'activation (ce n'est pas une des variables de la fonction), on doit aller la rechercher dans un bloc créé précédemment, en l'occurence dans le bloc d'activation créé par la fonction sous-jacente liée à &d (la fonction externe).
Continuons notre revue des fonctions de la barrière d'abstraction des environnements en étudiant les trois dernières fonctions (elles posent plus de problèmes que les deux premières), en commençant par le cas relativement simple de l'ajout d'associations variable -- valeurs. Nous avons utilisé deux fonctions:
| 492 |
;;; env-extension: Environnement * LISTE[Variable] * LISTE[Valeur] -> Environnement
;;; (env-extension env vars vals) rend l'environnement «env» étendu avec ;;; un bloc d'activation liant les variables «vars» aux valeurs «vals». |
| 503 |
;;; env-add-liaisons: LISTE[Liaison] * Environnement -> Environnement
;;; (env-add-liaisons liaisons env) rend l'environnement obtenu en ajoutant, ;;; à l'environnement «env», les liaisons «liaisons». |
Rappel: nous avons eu besoin de la fonction env-extension pour ajouter des liaisons variable --- valeur lors de l'écriture de la définition de la fonction fonction-creation et nous avons eu besoin de la fonction env-add-liaisons) pour ajouter des liaisons variable --- valeur lors de l'écriture de la définition de la fonction bloc-eval.
Remarquer que ces deux fonctions ont la même finalité mais qu'elles sont différentes de part leur signature: la fonction env-extension a comme données (autres que l'environnement) deux listes, la liste des variables et la liste des valeurs, alors que la fonction env-add-liaisons a comme donnée (autre que l'environnement) une seule liste, liste dont chaque élément est une association variable --- valeur.
Enfin, nous avons eu besoin de la fonction env-enrichissement pour ajouter des définitions fonctionnelles lors de l'écriture de la définition de la fonction corps-eval -- qui est appelée entre autres par bloc-eval:
| 516 |
;;; env-enrichissement: Environnement * LISTE[Definition] -> Environnement
;;; (env-enrichissement env defs) rend l'environnement «env» étendu avec un ;;; bloc d'activation pour les définitions fonctionnelles «defs». |
Précision: considérons l'« exemple » suivant d'un bloc où le corps possède deux définitions:
(let ()
(define (f1 x)
corps-f1)
(define (f2 y)
corps-f2)
exp-bloc)
(define (f1 x)
corps-f1)
(define (f2 y)
corps-f2)
exp-bloc)
Pour évaluer le corps, on doit évaluer exp-bloc dans l'environnement obtenu en enrichissant l'environnement courant avec les deux fonctions f1 et f2. Ces deux fonctions sont représentées par un 4-uplet formé du symbole *fonction*, de la liste des variables (i.e. '(x) -- resp. '(y)), du corps de la fonction (i.e corps-f1 -- resp. corps-f2) et de l'environnement, env dans lequel on doit évaluer les applications de ces deux fonctions.
Mais quel est l'environnement env? Question posée autrement: de quoi pouvons-nous nous servir dans le corps de f1? Bien sûr, de l'environnement où est évalué le corps (i.e. celui où est évalué le bloc, plus les liaisons définies derrière le let), mais pas seulement: f1 elle-même doit appartenir à l'environnement (cas de la récursivité), et aussi f2 (et plus généralement, tous les noms des fonctions définies dans le corps).
Mais cela veut dire que lorsque nous évaluons la définition de f1, nous devons le faire en utilisant un environnement où il y a f2 alors que nous ne savons même pas que f2 existe! Clairement, la possibilité d'utiliser quelque chose qui n'existe pas encore ne facilite pas l'écriture de l'évaluateur (de nombreux langages de programmation interdisent cela). On pourrait se dire que, pour simplifier cette écriture il suffit que, nous aussi, on l'interdise. Malheureusement, cette possibilité est absolument nécessaire si on veut pouvoir écrire des récursivités croisées (dans l'exemple si f1 apparaît dans corps-f2 et f2 apparaît dans corps-f1). Or, par exemple, c'est exactement ce que nous avons -- en plus complexe car il y en a de partout -- dans le présent logiciel; par exemple, evaluation appelle alternative-eval qui appelle evaluation.
Implantation (via barrière d'abstraction de bas niveau)
Afin que l'on puisse aller chercher une valeur (que ce soit de variable, que ce soit de fonction) dans un ajout antérieur, tout en donnant la priorité au derniers ajouts, on implante les environnements sous forme d'une suite de blocs d'activation, celui auquel on accède en premier étant celui qui est ajouté en dernier (en informatique, on parle de pile).
Définition de variable-val
L'idée de la définition de la fonction variable-val est alors très simple: on regarde si la variable est présente dans le premier bloc d'activation, auquel cas on va y chercher sa valeur et, si ce n'est pas le cas, on appelle récursivement la fonction sur le reste de l'environnement (i.e. l'environnement obtenu en supprimant le premier bloc d'activation). Et, bien sûr, pour que l'on puisse effectuer ce calcul, il faut qu'il y ait un bloc d'activation, autrement dit que l'environnement ne soit pas vide. D'où la définition:
| 480 |
;;; variable-val: Variable * Environnement -> Valeur
;;; (variable-val var env) rend la valeur de la variable «var» dans ;;; l'environnement «env». (define (variable-val var env) (if (env-non-vide? env) (let ((bloc (env-1er-bloc env))) (let ((variables (blocActivation-variables bloc))) (if (member var variables) (blocActivation-val bloc var) (variable-val var (env-reste env))))) (deug-erreur 'variable-val "variable inconnue" var) ) ) |
sous réserve que l'on ait, dans la barrière d'abstraction de bas niveau, les fonctions suivantes:
| 540 |
;;; env-non-vide?: Environnement -> bool
;;; (env-non-vide? env) rend #t ssi l'environnement «env» n'est pas vide |
| 551 |
;;; env-1er-bloc: Environnement -> BlocActivation
;;; ERREUR lorsque l'environnement donné est vide ;;; (env-1er-bloc env) rend le premier (i.e. celui qui a été ajouté en ;;; dernier) bloc d'activation de l'environnement «env». |
| 558 |
;;; env-reste: Environnement -> Environnement
;;; ERREUR lorsque l'environnement donné est vide ;;; (env-reste env) rend l'environnement obtenu en supprimant le premier ;;; bloc d'activation de l'environnement «env». |
et, dans la barrière d'abstraction des blocs d'activation,les fonctions suivantes:
| 570 |
;;; blocActivation-variables: BlocActivation -> LISTE[Variable]
;;; (blocActivation-variables bloc) rend la liste des variables définies ;;; dans le bloc d'activation «bloc» |
| 576 |
;;; blocActivation-val: BlocActivation * Variable -> Valeur
;;; HYPOTHESE: «var» est une variable définie dans «bloc» ;;; (blocActivation-val bloc var) rend la valeur de la variable «var» ;;; dans le bloc d'activation «bloc». |
Pour les fonctions qui ajoutent des blocs d'activation, commençons par celle qui enrichit l'environnement avec des définitions fonctionnelles car, étant la plus complexe, c'est elle qui détermine les fonctions de base utilisées.
Définition de env-enrichissement
Rappels
Pour une définition de fonction, on doit lier le nom de la fonction à une fonction du Scheme sous-jacent, fonction qui est défini par:
| 464 |
;;; fonction-creation: Definition * Environnement -> Fonction
;;; (fonction-creation definition env) rend la fonction définie par ;;; «definition» dans l'environnement «env». (define (fonction-creation definition env) (list '*fonction* (definition-variables definition) (definition-corps definition) env ) ) |
le problème étant que l'environnement env de la fonction précédente doit contenir toutes les fonctions définies dans le corps pour lequel on enrichi l'environnement avec la présente définition, y compris elle-même, y compris toute fonction dont la définition suit la définition que l'on est en train d'analyser). Gros problème : pour créer les différentes fonctions on doit utiliser un environnement qui ne sera défini que lorsque toutes les fonctions seront crées! On ne s'en sort pas! Eh bien si (mais je pense que vous vous en doutiez)!
Notons tout d'abord que la fonction que l'on est en train de définir ne sera réelement exécutée qu'après qu'on ait défini toutes les fonctions du corps, dans la partie <expressions> de ce corps, autrement dit après que l'on ait lu toutes les informations pour définir complètement l'environnement.
Remarque: on peut dire que c'est à cause de cela qu'en Scheme les parties définitions de fonctions et expressions sont séparées dans un corps. En passant, notons que ce n'est pas le cas au toplevel qui, encore une fois, a un statut particulier et rappelons que nous n'avons pas de tel toplevel en Deug-Scheme.
Idée
Comment allons nous faire? Considérons le « corps »:
(define (f ...) ...) ; def-f
(define (g ...) ...) ; def-g
(define (g ...) ...) ; def-g
Dans un premier temps, nous créons un bloc d'activation qui contient:
- la liste des variables de fonctions définies dans le bloc,
- autant de « cases » qu'il y a de variables définies dans le bloc, mais ces « cases » sont vides et il faudra ensuite les remplir avec la valeur des différentes fonctions (que nous calculerons en utilisant les définitions des fonctions).
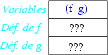
Nous pouvons alors ajouter cet environnement en tête de l'environnement courant:
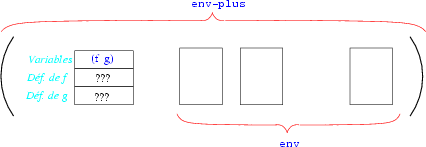
et nous pouvons alors définir les fonctions, du Scheme sous-jacent, qui implantent les deux fonctions:
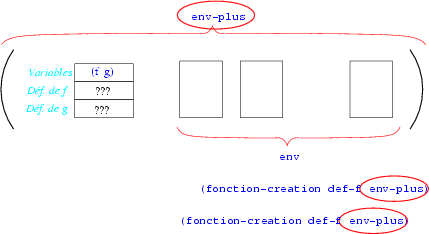
Noter bien que l'environnement utilisé dans les applications de fonction-creation est l'environnement env-plus créé précédemment, environnement où il y a les différentes fonctions définies dans le corps.
Et il ne reste plus qu'à remplir les cases non remplies du bloc d'activation:
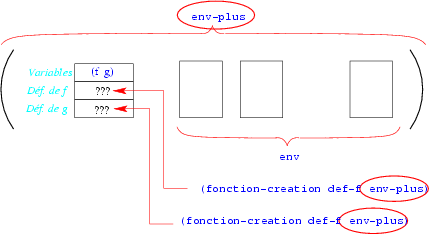
Noter que cette opération est une fonction très particulière puisqu'elle ne retourne pas de résultat (c'est comme les fonctions display et newline) et qu'elle modifie l'existant (au second semestre, on parlera de procédure). En Scheme, on parle tout de même de fonction -- ou plus exactement Scheme parle toujours de procédure -- mais le type du résultat est Rien et, par convention, le nom d'une telle fonction se termine par un point d'exclamation.
Pour mettre en oeuvre cette idée, nous avons besoin des fonctions suivantes:
Fonction de la barrière d'abstraction des environnements
| 545 |
;;; env-add: Environnement * BlocActivation -> Environnement
;;; (env-add bloc env) rend l'environnement obtenu en ajoutant devant ;;; l'environnement «env» le bloc d'activation «bloc». |
Fonctions de la barrière d'abstraction des blocs d'activation
| 584 |
;;; blocActivation-creation: LISTE[Variable] -> BlocActivation
;;; (blocActivation-creation vars) rend un bloc d'activation contenant ;;; la liste des variables «vars», avec la place qu'il faut pour les valeurs ;;; de ces variables, cette place n'étant pas remplie. |
| 594 |
;;; blocActivation-mettre-valeurs!: BlocActivation * LISTE[Valeur] -> Rien
;;; (blocActivation-mettre-valeurs! bloc vals) affecte les valeurs «vals» (données ;;; sous forme de liste) dans le bloc d'activation «bloc» (qui est un vecteur) |
Définition de env-enrichissement
La définition va alors de soi, en utilisant la fonction map, ou plutôt deug-map, et une fonction interne pour pouvoir appliquer cette denière:
| 516 |
;;; env-enrichissement: Environnement * LISTE[Definition] -> Environnement
;;; (env-enrichissement env defs) rend l'environnement «env» étendu avec un ;;; bloc d'activation pour les définitions fonctionnelles «defs». (define (env-enrichissement env defs) (let ((noms (deug-map definition-nom-fonction defs))) (let ((bloc (blocActivation-creation noms))) (let ((env-plus (env-add bloc env))) (define (fonction-creation-env-plus definition) (fonction-creation definition env-plus)) (begin (blocActivation-mettre-valeurs! bloc (deug-map fonction-creation-env-plus defs)) env-plus ) ) ) ) ) |
Définition de env-extension
La définition de cette fonction est plus simple que la précédente. On pourrait implanter cette fonction << d'un coup >> et non en deux étapes comme ci-dessus mais cela ajouterait des fonctions de base nécessaires et comme cela se fait bien comme ça... Ainsi on fabrique l'environnement résultat en
- créant un bloc d'activation de bonne taille et où la case de la liste des variables est remplie,
- remplissant les autres cases avec les valeurs:
| 492 |
;;; env-extension: Environnement * LISTE[Variable] * LISTE[Valeur] -> Environnement
;;; (env-extension env vars vals) rend l'environnement «env» étendu avec ;;; un bloc d'activation liant les variables «vars» aux valeurs «vals». (define (env-extension env vars vals) (if (= (length vars) (length vals)) (let ((bloc (blocActivation-creation vars))) (begin (blocActivation-mettre-valeurs! bloc vals) (env-add bloc env) ) ) (deug-erreur 'env-extension "arité incorrecte" (list vars vals)) ) ) |
Définition de env-add-liaisons
Nous avons déjà dit que cette fonction a la même sémantique que la précédente sauf qu'elle n'a pas la même signature (les liaisons sont données comme une liste d'associations alors que, dans la fonction prcédentes, les liaisons sont données par deux listes). Il suffit donc de fabriquer ces deux listes et d'appliquer la fonction précédente:
- la détermination de la liste des variables se fait facilement en utilisant la fonction deug-map appliquée sur la fonction liaison-variable qui, étant donnée une liaison, retourne la variable liée,
- la détermination de la liste des valeurs s'effectue en deux
applications de la fonction deug-map:
- la première « mappe » la liste des liaisons avec la fonction liaison-exp (qui, étant donnée une liaison, retourne l'expression de la valeur de la variable liée),
- la seconde « mappe » la liste ainsi obtenue avec une fonction qui évalue ces expressions dans l'environnement donné (on a donc besoin d'une fonction interne):
| 503 |
;;; env-add-liaisons: LISTE[Liaison] * Environnement -> Environnement
;;; (env-add-liaisons liaisons env) rend l'environnement obtenu en ajoutant, ;;; à l'environnement «env», les liaisons «liaisons». (define (env-add-liaisons liaisons env) ;; eval-env : Expression -> Valeur ;; (eval-env exp) rend la valeur de «exp» dans l'environnement «env» (define (eval-env exp) (evaluation exp env)) ;; expression de (env-add-liaisons liaisons env) : (env-extension env (deug-map liaison-variable liaisons) (deug-map eval-env (deug-map liaison-exp liaisons)) ) ) |
Implantation barrière d'abstraction de bas niveau
Rappel de la spécification
| 536 |
;;; env-vide: -> Environnement
;;; (env-vide) rend l'environnement vide |
| 540 |
;;; env-non-vide?: Environnement -> bool
;;; (env-non-vide? env) rend #t ssi l'environnement «env» n'est pas vide |
| 545 |
;;; env-add: Environnement * BlocActivation -> Environnement
;;; (env-add bloc env) rend l'environnement obtenu en ajoutant devant ;;; l'environnement «env» le bloc d'activation «bloc». |
| 551 |
;;; env-1er-bloc: Environnement -> BlocActivation
;;; ERREUR lorsque l'environnement donné est vide ;;; (env-1er-bloc env) rend le premier (i.e. celui qui a été ajouté en ;;; dernier) bloc d'activation de l'environnement «env». |
| 558 |
;;; env-reste: Environnement -> Environnement
;;; ERREUR lorsque l'environnement donné est vide ;;; (env-reste env) rend l'environnement obtenu en supprimant le premier ;;; bloc d'activation de l'environnement «env». |
Structure de données
Environnement = LISTE[BlocActivation]
Définition des fonctions
Trop facile, laissée en exercice.
Implantation barrière d'abstraction des blocs d'activation
Rappel de la spécification
| 570 |
;;; blocActivation-variables: BlocActivation -> LISTE[Variable]
;;; (blocActivation-variables bloc) rend la liste des variables définies ;;; dans le bloc d'activation «bloc» |
| 576 |
;;; blocActivation-val: BlocActivation * Variable -> Valeur
;;; HYPOTHESE: «var» est une variable définie dans «bloc» ;;; (blocActivation-val bloc var) rend la valeur de la variable «var» ;;; dans le bloc d'activation «bloc». |
| 584 |
;;; blocActivation-creation: LISTE[Variable] -> BlocActivation
;;; (blocActivation-creation vars) rend un bloc d'activation contenant ;;; la liste des variables «vars», avec la place qu'il faut pour les valeurs ;;; de ces variables, cette place n'étant pas remplie. |
| 594 |
;;; blocActivation-mettre-valeurs!: BlocActivation * LISTE[Valeur] -> Rien
;;; (blocActivation-mettre-valeurs! bloc vals) affecte les valeurs «vals» (données ;;; sous forme de liste) dans le bloc d'activation «bloc» (qui est un vecteur) |
Structure de données
Comment créer des « cases » vides que l'on peut remplir ensuite ? Pour ce faire, il existe en Scheme la notion de vecteur. D'où:
BlocActivation = VECTEUR[LISTE[Variable] Valeur...]
Un vecteur est une suite de cases numérotées (à partir de 0) et on peut:
1 - créer un vecteur, ayant un nombre de cases donné, les cases n'étant pas remplies, avec la fonction make-vector:
;;; make-vector : nat -> VECTEUR[alpha]
;;; (make-vector taille) rend un vecteur de dimension "taille"
;;; (make-vector taille) rend un vecteur de dimension "taille"
2 - affecter une valeur à une case désignée par son numéro d'ordre -- rappelons que la première case a comme numéro 0:
;;; vector-set! : VECTEUR[alpha] * nat * alpha -> Rien
;;; (vector-set! v i val) affecte au ("i"+1)'ème élément de "v" la
;;; valeur "val". Par exemple, "(vector-set! v 0 val)" affecte au
;;; premier élément de "v" la valeur "val".
;;; (vector-set! v i val) affecte au ("i"+1)'ème élément de "v" la
;;; valeur "val". Par exemple, "(vector-set! v 0 val)" affecte au
;;; premier élément de "v" la valeur "val".
Notons que cette fonction Scheme ne retourne pas de résultat et qu'elle modifie un de ses arguments. Rappelons que le type du résultat est alors Rien et que, par convention, le nom se termine par un point d'exclamation.
2 - connaître la valeur contenue dans une case:
;;; vector-ref : VECTEUR[alpha] * nat -> alpha
;;; (vector-ref v i) retourne le ("i"+1)'ème élément du vecteur "v".
;;; Par exemple, "(vector-ref v 0)" retourne le premier élément
;;; de "v", "(vector-ref v 1)" retourne le deuxième élément...
;;; (vector-ref v i) retourne le ("i"+1)'ème élément du vecteur "v".
;;; Par exemple, "(vector-ref v 0)" retourne le premier élément
;;; de "v", "(vector-ref v 1)" retourne le deuxième élément...
Définitions des fonctions de la barrière d'abstraction
Définition de blocActivation-variables
Trés simple puisque c'est le contenu de la première case du vecteur:
| 570 |
;;; blocActivation-variables: BlocActivation -> LISTE[Variable]
;;; (blocActivation-variables bloc) rend la liste des variables définies ;;; dans le bloc d'activation «bloc» (define (blocActivation-variables bloc) (vector-ref bloc 0) ) |
Définition de blocActivation-val
L'idée est très simple: on cherche le rang, i, de la variable dans la liste des variables et il ne reste plus qu'à rendre le contenu de la ième case du vecteur:
| 576 |
;;; blocActivation-val: BlocActivation * Variable -> Valeur
;;; HYPOTHESE: «var» est une variable définie dans «bloc» ;;; (blocActivation-val bloc var) rend la valeur de la variable «var» ;;; dans le bloc d'activation «bloc». (define (blocActivation-val bloc var) (let ((i (rang var (blocActivation-variables bloc)))) (vector-ref bloc i) ) ) |
Définition de blocActivation-creation
Très simple (ne pas oublier de remplir la case 0):
| 584 |
;;; blocActivation-creation: LISTE[Variable] -> BlocActivation
;;; (blocActivation-creation vars) rend un bloc d'activation contenant ;;; la liste des variables «vars», avec la place qu'il faut pour les valeurs ;;; de ces variables, cette place n'étant pas remplie. (define (blocActivation-creation vars) (let ((bloc (make-vector (+ 1 (length vars))))) (begin (vector-set! bloc 0 vars) bloc ) ) ) |
Définition de blocActivation-mettre-valeurs!
Pour assigner les valeurs, la difficulté vient du fait que l'on ne sait pas combien il y en a: on doit donc définir une fonction (interne) récursive qui remplit les cases d'un vecteur, à partir d'un indice donné, avec les éléments successifs d'une liste donnée et appliquer cette fonction avec comme indice initial 1 (premier indice où l'on trouve une valeur) et la liste de valeurs.
| 594 |
;;; blocActivation-mettre-valeurs!: BlocActivation * LISTE[Valeur] -> Rien
;;; (blocActivation-mettre-valeurs! bloc vals) affecte les valeurs «vals» (données ;;; sous forme de liste) dans le bloc d'activation «bloc» (qui est un vecteur) (define (blocActivation-mettre-valeurs! bloc vals) ;; remplir!: nat * LISTE[Valeur] -> Rien ;; (remplir! i vals) remplit les cases du vecteur «bloc», à partir de ;; l'indice «i», avec les valeurs de la liste «vals» (et dans le même ordre). (define (remplir! i vals) (if (pair? vals) (begin (vector-set! bloc i (car vals)) (remplir! (+ i 1) (cdr vals)) ) ) ) (remplir! 1 vals) ) |
Environnement initial
Pour créer l'environnement initial il suffit d'étendre l'environnement vide avec des liaisons nom-de-la-primitive --- valeur-de-la-primitive. Pour ce faire, nous pouvons penser utiliser la fonction env-extension ou la fonction env-add-liaisons. Nous décidons d'utiliser env-extension (comme exercice, vous pouvez essayer de le faire avec env-add-liaisons; attention, une liaison est une association variable --- expression et env-add-liaisons évalue les expressions).
C'est rrès facile (vous pouvez essayer)... sauf qu'il faut écrire (décrire) les primitives avec deux listes: la première qui contient les différents noms et la seconde qui contient les différentes valeurs, la première valeur correspondant au premier nom, la seconde valeur correspondant au second nom... la 27ème valeur correspondant au 27ème nom et gare à celui qui intervertit deux noms ou deux valeurs!
Description des primitives
Aussi, pour éviter des erreurs, nous décrivons chaque primitive par quatre éléments, le nom d'une primitive, la fonction correpondante du Scheme sous-jacent et l'arité représentée par un comparateur et un entier et nous fabriquerons une desciption -- implantée par un n-uplet -- de la primitive en utilisant la fonction description-primitive:
| 633 |
;;; description-primitive: Variable * (Valeur ... -> Valeur)
;;; * (num * num -> bool) * num -> DescriptionPrimitive ;;; (description-primitive var f comparator arite) rend la description de la ;;; primitive désignée par «var», implantée dans le Scheme sous-jacent par «f» et ;;; dont l'arité est définie par «comparator» «arite». (define (description-primitive var f comparator arite) (list var f comparator arite)) |
Les primitives sont alors données comme une liste de description sous une forme très lisible (voir lignes 641 à 674 ):
| 641 |
;;; descriptions-primitives: -> LISTE[DescriptionPrimitive]
;;; (descriptions-primitives) rend la liste des descriptions de toutes les ;;; primitives
(define (descriptions-primitives)
...(cons (description-primitive 'car car = 1)
(cons (description-primitive 'erreur erreur >= 2)
|
| 674 |
'())))))))))))))))))))))))))))))) )
|
Noter que nous avons utilisé cons (et non list qui nous aurait facilité la tâche) car, si nous avions utilisé list, pour l'auto-évaluation, il aurait fallu que les primitives ayant un nombre quelconque d'arguments puissent être appelées avec au moins une trentaine d'arguments (voir ce que cela implique pour l'imlantation de la fonction primitive-invocation...).
Définition de la fonction env-initial
Comme nous l'avons déja dit, il faut créer les deux listes (celle des variables et celle des valeurs) à partir de cette liste. Bien sûr, nous le faisons en utilisant deug-map (et même deux fois pour calculer les valeurs).
| 624 |
;;; env-initial: -> Environnement
;;; (env-initial) rend l'environnement initial, i.e. l'environnement qui ;;; contient toutes les primitives. (define (env-initial) (env-extension (env-vide) (deug-map car (descriptions-primitives)) (deug-map primitive-creation (deug-map cdr (descriptions-primitives)) ) ) ) |


