Notion de grammaire
Avant de parler de grammaire, donnons le sens que nous utiliserons pour les mots « expression » et « langage ». Une expression est une représentation textuelle d'un calcul. L'ensemble des expressions utilisables est un langage.
Exemples de grammaires des langages des expressions booléennes simples
Comme premier exemple, étudions les expressions booléennes simples (i.e. la disjonction et la conjonction sont de opérateurs binaires), avec variables.
Comme nous l'avons rappelé dans le paragraphe ??, page ??, il existe plusieurs écritures d'une expression selon le placement de l'opérateur par rapport à ses opérandes (écriture infixe, préfixe...) et selon le status des parenthèses (écriture sans parenthèse, complètement parenthésée...). Nous donnons ci-dessous quatre définitions, à l'aide de grammaires, de langages des expressions booléennes simples.
En infixé, complètement parenthésée
Voici la grammaire des expressions booléennes simples avec variables en infixé complètement parenthésée:
| <expBoolSimpleinfixe> | -> | <atomique> |
| <unaire> | ||
| <binaire> | ||
| <unaire> | -> | ( <opérateur1> <expBoolSimpleinfixe> ) |
| <binaire> | -> | ( <expBoolSimpleinfixe> <opérateur2> <expBoolSimpleinfixe> ) |
| <atomique> | -> | <constante> |
| <variable> | ||
| <constante> | -> | @f | faux |
| @v | vrai | ||
| <variable> | -> | Une suite de caractères autres que l'espace, les parenthèses et @ |
| <opérateur1> | -> | @non |
| <opérateur2> | -> | @et | et |
| @ou | ou | ||
Terminologie:
- <expBoolSimpleinfixe>, <constante>... sont des non-terminaux ou unités syntaxiques de la grammaire; ils ne seront jamais écrits tels quels, on les dérivera (cf. plus loin);
- @f, @v, @non, @et et @ou sont des éléments terminaux de la grammaire; ils sont écrits tels quels dans le langage;
- Une suite de caractères autres que l'espace, les parenthèses et @ est aussi un élément terminal mais, contrairement aux précédents, on le décrit de façon informelle;
- <expBoolSimpleinfixe>, qui est la première unité syntaxique définie, est l'axiome de la grammaire: c'est d'elle dont on part pour définir un mot du langage.
Remarque: nous voulons écrire des fonctions Scheme manipulant des mots du langage, aussi avons-nous dû choisir des graphismes utilisables sur ordinateur: les opérateurs booléens classiques, Ù, Ú et ¬, ont été remplacés par @et, @ou et @non. D'autre part, pour bien distinguer les variables (que l'on a tendance à noter v) des constantes booléennes, nous avons noté ces dernières @f et @v. Noter que nous n'avons pas pris #f et #t car nous voulons bien distinguer le langage Scheme et notre langage des expressions booléennes.
« À la Scheme »
On peut aussi décider d'écrire les expressions « à la Scheme » (i.e. en préfixé, complètement parenthésées):
| <expBoolSimpleScheme> | -> | <atomique> |
| <unaire> | ||
| <binaire> | ||
| <unaire> | -> | ( <opérateur1> <expBoolSimpleScheme> ) |
| <binaire> | -> | ( <opérateur2> <expBoolSimpleScheme> <expBoolSimpleScheme> ) |
| <atomique> | -> | <constante> |
| <variable> | ||
| <constante> | -> | @f | faux |
| @v | vrai | ||
| <variable> | -> | Une suite de caractères autres que l'espace, les parenthèses et @ |
| <opérateur1> | -> | @non |
| <opérateur2> | -> | @et | et |
| @ou | ou | ||
En polonaise préfixée
On peut aussi décider d'écrire les expressions en polonaise préfixée (sans parenthèse):
| <expBoolSimplepolonaise> | -> | <atomique> |
| <unaire> | ||
| <binaire> | ||
| <unaire> | -> | <opérateur1> <expBoolSimplepolonaise> |
| <binaire> | -> | <opérateur2> <expBoolSimplepolonaise> <expBoolSimplepolonaise> |
| <atomique> | -> | <constante> |
| <variable> | ||
| <constante> | -> | @f | faux |
| @v | vrai | ||
| <variable> | -> | Une suite de caractères autres que l'espace, les parenthèses et @ |
| <opérateur1> | -> | @non |
| <opérateur2> | -> | @et | et |
| @ou | ou | ||
En notation « normale »
| <expBoolSimplenormale> | -> | <atomique> |
| <unaire> | ||
| <binaire> | ||
| ( <expBoolSimplenormale> ) | ||
| <unaire> | -> | <opérateur1> <expBoolSimplenormale> |
| <binaire> | -> | <expBoolSimplenormale> <opérateur2> <expBoolSimplenormale> |
| <atomique> | -> | <constante> |
| <variable> | ||
| <constante> | -> | @f | faux |
| @v | vrai | ||
| <variable> | -> | Une suite de caractères autres que l'espace, les parenthèses et @ |
| <opérateur1> | -> | @non |
| <opérateur2> | -> | @et | et |
| @ou | ou | ||
Exemple 1: @non (@v @et @v) @ou @f
Exemple 2: @non @v @et (@v @ou @f)
Exemple 3: @non @v @et @v @ou @f
Remarques:
-
Pour savoir comment calculer l'expression
@non @v @et @v @ou @f,
il faut savoir qu'elle est équivalente à
((@non @v) @et @v) @ou @f.
Pour ce faire, on doit, en plus de la grammaire, donner des règles
de priorités: ici, pour suivre les conventions classiques, nous
décidons que le « @non » est plus prioritaire que le « @et »
lui-même plus prioritaire que le « @ou ». Ces règles de priorités
imposent de parenthéser d'abord les sous-expressions correspondant à
un « @non » et, ensuite, celles qui correspondent à un « @et »
(et on n'a pas besoin de parenthéser les sous-expressions qui
correspondent à « @ou » car c'est la priorité la plus faible).
Ainsi, dans l'exemple @non @v @et @v @ou @f,
- il y a un « @non » (opérateur unaire): cette expression est équivalente à (@non @v) @et @v @ou @f,
- il y a un « @et » (opérateur binaire): cette expression est équivalente à ((@non @v) @et @v) @ou @f.
- La règle
<expBoolSimplenormale> -> ( <expBoolSimplenormale> )
permet alors de parenthéser des sous-expressions qui, sinon, seraient découpées autrement par les règles de priorités (par exemple @non (@v @et @v) @ou @f.
Notes didactiques:
- ce langage est étudié parce que ce sont les expressions booléennes que vous avez l'habitude d'utiliser par ailleurs;
- la description du langage que nous avons donné ci-dessus utilise autre chose (la notion de priorité) que la notion de grammaire;
- il existe des grammaires auto-suffisantes pour ce langage mais elles s'éloignent de la forme des grammaires que nous avons données pour décrire les autres langages des expressions booléennes simples et, surtout, elles demandent une réflexion approfondie sur les grammaires, étude qui dépasse le cadre de cet ouvrage.
Similitude des différents ensembles de règles de grammaire
On peut noter que toutes ces grammaires ont des points en commun, points en commun que nousretrouverions dans tous les langages des expressions booléennes simples:
- les règles pour les expressions atomiques sont exactement les mêmes,
- surtout, les règles pour les expressions binaires disent que
l'on doit décomposer l'expression avec:
- un opérateur (qui peut être à différentes places selon le langage),
- qui a deux opérandes qui sont des expressions (que l'on devra donc aussi décomposer),
- de même, les règles pour les expressions unaires disent
toutes que l'on doit décomposer l'expression avec:
- un opérateur (qui peut être à différentes places selon le langage),
- qui a un opérande qui est une expression (que l'on devra donc aussi décomposer).
On peut donc parler d'une classe de langages définis par une classe de grammaires (ou par une classe de langages définie par une classe de grammaires).
Génération d'un mot du langage
Considérons un langage de la classe des langages des expressions booléennes simple, par exemple celui des expressions écrites en infixé, complètement parenthésé.
Le langage défini par une grammaire est égal à l'ensemble des mots (ou, si vous préférez, expressions) que l'on peut générer à l'aide de la grammaire.
Notation: dans les schémas de ce paragraphe, pour des raisons de mise en page, les unités syntaxiques <expBoolSimpleinfixe>, <atomique>, <constante>, <opérateur1> et <opérateur2> sont renommées respectivement <expr>, <atom>, <cste>, <op1> et <op2>.
Pour générer un mot du langage à partir de la grammaire, on part de l'axiome (rappelons que c'est la première unité syntaxique définie dans la grammaire), ici <expBoolSimpleinfixe> que nous avons renommé <expr>:

et on la dérive, c'est-à-dire que l'on prend une des possibilités de la règle et qu'on remplace l'axiome par le membre droit de cette possibilité. Par exemple, en prenant la troisième possibilité:

<binaire> est un non-terminal: on doit effectuer la dérivation (il n'y a qu'une possibilité):

les deux parenthèses sont des terminaux: on ne les touche pas; en revanche, on dérive comme ci-dessus les non-terminaux <expr>, <op2> et <expr> (remarquez que l'axiome joue le même rôle que n'importe quel non-terminal, sauf au départ). Prenons la deuxième possibilité pour le premier <expr>, la seconde possibilité pour <op2> et la première possibilité pour le second <expr>:

@et est un terminal: on ne le touche pas; dérivons les terminaux <unaire> (il n'y a qu'une posibilité) et <atom> (qui correspond à <atomique>) en prenant la première possibilité:

pour <op1>, il n'y a qu'une possibilité; pour <expr>, décidons de prendre la troisième possibilité; pour <cste> (qui correspond à <constante>), prenons la première possibilité:

le seul non-terminal est <binaire> et il n'y a qu'une possibilité:
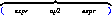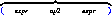
décidons de prendre la première possibilité pour les deux occurrences de <expr> et la première possibilité pour <op2>:

décidons de prendre la première possibilité pour les deux occurrences de <atom>:

et enfin dérivons les deux occurrences du non-terminal <cste> en prenant la seconde possibilité dans les deux cas:

Toutes les dérivations ont été effectuées (il ne reste plus de non-terminaux en suspens). Pour connaître le mot généré, il suffit de lire de gauche à droite les terminaux:

Constructeurs
Par programme, on ne génère pas l'ensemble des mots du langage, mais on construit souvent des mots du langage (par exemple, dans la suite de cet ouvrage, on simplifiera des expressions: il s'agit de construire une expression à partir d'une expression donnée).
Pour ce faire, on doit pouvoir effectuer exactement ce que nous avons fait « à la main » lorsque nous avons généré un mot à partir de la grammaire. Autrement dit, nous devons pouvoir écrire des constantes (vrai et faux), des variables, des opérateurs (non, et, ou) et des expressions composées (unaires et binaires), ce qui sera fait en utilisant des constructeurs ( ebs-constante-vrai, ebs-constante-faux, ebs-variable, ebs-unaire, ebs-binaire, ebs-operateur1-non, ebs-operateur2-et et ebs-operateur2-ou).
Règles de nomenclature: pour faciliter la lecture des programmes (et donc leur écriture), il est important de se donner, et de suivre, des règles pour le choix des noms des fonctions. Nous préciserons plus loin les différentes règles que nous suivons, mais notons tout de suite que, systématiquement, les noms des fonctions utiles pour un langage seront préfixés par le nom abrégé du langage (ici « ebs- » pour « expressions booléennes simples »).
Analyse d'un mot
Les grammaires sont utilisées, particulièrement en informatique, pour savoir si un mot (une phrase) appartient bien à un certain langage (penser aux langages de programmation, aux langages de commande...) et pour effectuer une certaine tâche lorsque c'est le cas. On nomme analyse d'un mot la décomposition de ce mot, décomposition effectuée pour savoir si le mot appartient au langage ou pour déterminer la tâche qu'il exprime.
Dans ce paragraphe, nous voudrions voir comment écrire un programme qui réalise cette analyse. Pour ce faire, regardons comment on pourrait analyser « à la main » un mot du langage, en dégageant les fonctions qui seront nécessaires pour écrire un tel programme d'analyse.
Reconnaisseurs
Supposons que l'on veuille savoir si
((@non (@v @et @v)) @ou @f)
est un mot du langage engendré par la grammaire précédente. Pour que ce soit le cas, il faut qu'il dérive de l'axiome <expBoolSimpleinfixe>:
?? <expBoolSimpleinfixe> devient ((@non (@v @et @v)) @ou @f)??
La règle de <expBoolSimpleinfixe> fournit trois possibilités. Laquelle choisir? Ici,
- on voit facilement que le mot ne peut pas dériver du non-terminal <atomique> (car les mots qui dérivent de ce non terminal ne commencent pas par une parenthèse ouvrante),
- on peut voir qu'il ne peut pas dériver du non-terminal <unaire> (car le second caractère d'un tel mot est toujours un « @ »),
- on peut voir qu'il est possible qu'il dérive du non-terminal <binaire>.
Si l'on veut écrire un programme qui analyse un mot afin de déterminer s'il appartient au langage engendré par la grammaire, il faut avoir des fonctions pour décider dans quel cas on est. On nomme ces fonctions -- qui sont des prédicats -- des reconnaisseurs.
Par exemple, avec notre grammaire des expressions booléennes simples, nous devons avoir les reconnaisseurs ebs-atomique?, ebs-unaire? et ebs-binaire?.
Attention, en général, on ne peut pas demander que les reconnaisseurs soient infaillibles, tout en exigeant que le programme d'analyse, lui, le soit. Pour s'en convaincre il suffit de se dire que la définition de la fonction d'analyse serait alors triviale (or cela se saurait si la définition des fonctions d'analyse était triviale: c'est un problème qui a occupé de nombreux chercheurs dans les années 50 et 60):
(define (ebs-infixe? m)
(or (ebs-atomique? m) (ebs-unaire? m) (ebs-binaire? m)))
(or (ebs-atomique? m) (ebs-unaire? m) (ebs-binaire? m)))
(cond ((ebs-atomique? exp)
; expression de la valeur à rendre lorsque exp dérive de <atomique>
)
((ebs-unaire? exp)
; expression de la valeur à rendre lorsque exp dérive de <unaire>
)
((ebs-binaire? exp)
; expression de la valeur à rendre lorsque exp dérive de <binaire>
)
(else (erreur 'fn "donnée pas bien formée")))
; expression de la valeur à rendre lorsque exp dérive de <atomique>
)
((ebs-unaire? exp)
; expression de la valeur à rendre lorsque exp dérive de <unaire>
)
((ebs-binaire? exp)
; expression de la valeur à rendre lorsque exp dérive de <binaire>
)
(else (erreur 'fn "donnée pas bien formée")))
Accesseurs
Revenons à l'analyse, « à la main », du mot ((@non (@v @et @v)) @ou @f). Nous avons dit que ce mot ne pouvait dériver que du non-terminal <binaire>. Regardons si c'est possible:
?? <binaire> devient ((@non (@v @et @v)) @ou @f)??
La règle de <binaire> ne comporte qu'une possibilité: il n'y a donc pas de problème de choix. Le mot et la partie droite commencent par une parenthèse ouvrante (cela correspond donc) et elles finissent par une parenthèse fermante (cela correspond toujours) mais, dans la partie droite de la règle, il reste <expBoolSimpleinfixe> <opérateur2> <expBoolSimpleinfixe> qu'il faut faire correspondre avec (@non (@v @et @v)) @ou @f.
À la main, on voit que la décomposition doit être (@non (@v @et @v)) pour la première occurrence de <expBoolSimpleinfixe>, @ou pour <opérateur2> et @f pour la seconde occurrence de <expBoolSimpleinfixe>.
Si l'on veut écrire un programme il faut que l'on ait des fonctions pour accéder aux différents éléments de cette décomposition. On nomme accesseurs de telles fonctions. Ainsi, dans notre exemple, nous avons besoin des accesseurs ebs-binaire-operande-gauche, ebs-binaire-operande-droit et ebs-binaire-operateur.
Et on continue en analysant (@non (@v @et @v))) (qui doit dériver de <expBoolSimpleinfixe>), @ou (qui doit dériver de <opérateur2>) et @f (qui doit dériver de <expBoolSimpleinfixe>):
?? <expBoolSimpleinfixe> devient (@non (@v @et @v)))??
...
?? <opérateur2> devient @ou??
...
?? <expBoolSimpleinfixe> devient @f??
...


