Fonctions de lecture et d'écriture
Une fonction manipulant les expressions booléennes simples peut avoir comme donnée ou comme résultat une expression booléenne simple:
- Lorsque la fonction rend une expression booléenne simple, au moins pour la tester, il faut pouvoir afficher une telle expression (rappelons que dans l'implantation que nous vous fournissons, toutes les expressions sont affichées avec un point rouge).
- Lorsque la fonction a comme donnée une expression booléenne simple, jusqu'à présent, pour la tester, nous avons « fabriqué » une telle expression booléenne en utilisant les constructeurs de la barrière syntaxique. Or, l'intérêt d'avoir un langage est d'utiliser des mots du langage comme données à de telles fonctions.
Considérons le cas d'une fonction, f, qui regroupe tous les problèmes, à savoir que la donnée et le résultat de la fonction sont des expressions booléennes simples:
Pour tester cette fonction, actuellement, travaillant uniquement avec la barrière syntaxique, la donnée doit être fournie uniquement à l'aide des constructeurs et l'affichage est, systématiquement, un point rouge (il faut être un expert plus que confirmé pour savoir si c'est le bon résultat...):
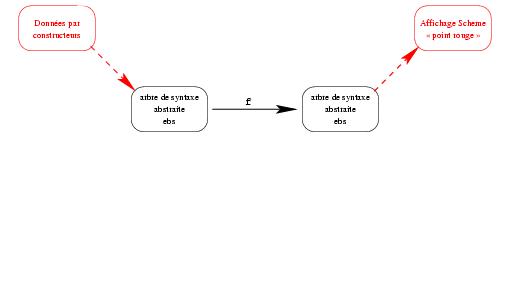
Le but de cette section est d'écrire différentes fonctions de conversion pour pouvoir
- dans les programmes, écrire les données dans un langage lisible par l'homme (et comme les données sont des expressions booléennes simples, nous utiliserons des langages des expressions booléennes simples),
- convertir, pour que ce soit lisible par l'homme, des expressions booléennes simples dans un des langages des expressions booléennes simples:
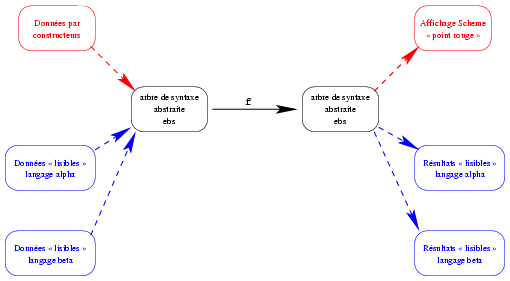
Dans un premier temps, nous regardons comment convertir une expression booléenne simple en une expression lisible par l'homme (c'est facile, nous aurions pu le laisser en exercice). Dans un deuxième temps, nous regarderons la conversion d'une donnée lisible par l'homme en une expression booléenne simple.
Fonctions de conversion de sortie
La conversion est particulièrement simple si on se contente d'une forme complètement parenthésée car on a alors une Sexpression, structure que Scheme affiche parfaitement. Comme exercice, vous pouvez écrire les différentes fonctions (en préfixé, infixé et suffixé). Nous donnons ci-dessous une définition de la fonction qui convertit l'expression en préfixé (complètement parenthésée).
Conversion en préfixé (complètement parenthésée)
Nous nommons cette fonction ebs->sexpr-pref car sa donnée est une expression booléenne simple (d'où ebs->) et que son résultat est une Sexpression (d'où sexpr) représentant l'expression booléenne simple en préfixé (d'où pref).
Spécification
Sa spécification est:
;;; ebs->sexpr-pref : ExprBoolSimple -> Sexpression
;;; (ebs->sexpr-pref exp) rend la Sexpression représentant exp en
;;; notation préfixée, complètement parenthésée.
;;; (ebs->sexpr-pref exp) rend la Sexpression représentant exp en
;;; notation préfixée, complètement parenthésée.
Exemple d'application
(let ((expression
(ebs-binaire (ebs-unaire (ebs-operateur1-non)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-et)
(ebs-constante-vrai)))
(ebs-operateur2-et)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-ou)
(ebs-constante-faux)))))
(ebs->sexpr-pref expression))
(ebs-binaire (ebs-unaire (ebs-operateur1-non)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-et)
(ebs-constante-vrai)))
(ebs-operateur2-et)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-ou)
(ebs-constante-faux)))))
(ebs->sexpr-pref expression))
-> (@et (@non (@et @v @v)) (@ou @v @f))
Implantation
Comme pour toutes les fonctions dont la donnée est un mot du langage, la forme générale de la définition de ebs->sexpr-pref est une conditionnelle qui passe en revue toutes les branches de la règle donnée pour l'axiome (rappelons que c'est la première règle):
(define (ebs->sexpr-pref exp)
(cond ((ebs-atomique? exp)
... à faire
((ebs-unaire? exp)
... à faire
... à faire
((ebs-binaire? exp)
... à faire
... à faire
... à faire
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
(cond ((ebs-atomique? exp)
... à faire
((ebs-unaire? exp)
... à faire
... à faire
((ebs-binaire? exp)
... à faire
... à faire
... à faire
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
et il n'y a plus qu'à remplir les trous. Lorsque l'expression est réduite à une constante, la forme préfixe est l'expression elle-même:
(define (ebs->sexpr-pref exp)
(cond ((ebs-atomique? exp)
exp)
((ebs-unaire? exp)
... à faire
... à faire
((ebs-binaire? exp)
... à faire
... à faire
... à faire
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
(cond ((ebs-atomique? exp)
exp)
((ebs-unaire? exp)
... à faire
... à faire
((ebs-binaire? exp)
... à faire
... à faire
... à faire
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
lorsque l'expression donnée est une expression unaire, sa forme préfixe est obtenue en écrivant l'opérateur unaire suivi de la forme préfixe de la sous-expression, le tout entre parenthèses (qui sont données par la liste):
(define (ebs->sexpr-pref exp)
(cond ((ebs-atomique? exp)
exp)
((ebs-unaire? exp)
(list (ebs-unaire-operateur exp)
(ebs->sexpr-pref (ebs-unaire-operande exp))))
((ebs-binaire? exp)
... à faire
... à faire
... à faire
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
(cond ((ebs-atomique? exp)
exp)
((ebs-unaire? exp)
(list (ebs-unaire-operateur exp)
(ebs->sexpr-pref (ebs-unaire-operande exp))))
((ebs-binaire? exp)
... à faire
... à faire
... à faire
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
lorsque l'expression donnée est une expression binaire, sa forme préfixe est obtenue en écrivant l'opérateur binaire suivi de la forme préfixe de la sous-expression gauche suivi de la forme préfixe de la sous-expression droite, le tout entre parenthèses (qui sont données par la liste):
(define (ebs->sexpr-pref exp)
(cond ((ebs-atomique? exp)
exp)
((ebs-unaire? exp)
(list (ebs-unaire-operateur exp)
(ebs->sexpr-pref (ebs-unaire-operande exp))))
((ebs-binaire? exp)
(list (ebs-binaire-operateur exp)
(ebs->sexpr-pref (ebs-binaire-operande-gauche exp))
(ebs->sexpr-pref (ebs-binaire-operande-droit exp))))
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
(cond ((ebs-atomique? exp)
exp)
((ebs-unaire? exp)
(list (ebs-unaire-operateur exp)
(ebs->sexpr-pref (ebs-unaire-operande exp))))
((ebs-binaire? exp)
(list (ebs-binaire-operateur exp)
(ebs->sexpr-pref (ebs-binaire-operande-gauche exp))
(ebs->sexpr-pref (ebs-binaire-operande-droit exp))))
(else (erreur 'ebs->sexpr-pref
"expression mal formée"))))
Conversion en polonaise préfixé
Une expression en polonaise préfixé n'étant pas parenthésée, le résultat de la fonction permettant l'affichage n'est pas une Sexpression, mais une chaîne de caractères et nous nommerons ebs->string-pol-pref cette fonction.
Spécification
Sa spécification est:
;;; ebs->string-pol-pref : ExprBoolSimple -> Sexpression
;;; (ebs->string-pol-pref exp) rend la Sexpression représentant exp en
;;; notation préfixée, complètement parenthésée.
;;; (ebs->string-pol-pref exp) rend la Sexpression représentant exp en
;;; notation préfixée, complètement parenthésée.
Exemple d'application
(let ((expression
(ebs-binaire (ebs-unaire (ebs-operateur1-non)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-et)
(ebs-constante-vrai)))
(ebs-operateur2-et)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-ou)
(ebs-constante-faux)))))
(ebs->string-pol-pref expression))
(ebs-binaire (ebs-unaire (ebs-operateur1-non)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-et)
(ebs-constante-vrai)))
(ebs-operateur2-et)
(ebs-binaire (ebs-constante-vrai)
(ebs-operateur2-ou)
(ebs-constante-faux)))))
(ebs->string-pol-pref expression))
-> "@et @non @et @v @v @ou @v @f"
Implantation
Tout d'abord, notez que, dans la notation polonaise, comme nous pouvons écrire les variables avec plusieurs caractères, les différents éléments doivent être isolés. En effet, par exemple, Úabc (ou @ouabc) est ambigu (est-ce Úa bc ou Úab c?).
L'implantation ne pose pas de problème:
;;; ebs->string-pol-pref : ExprBoolSimple -> Sexpression
;;; (ebs->string-pol-pref exp) rend la Sexpression représentant exp en
;;; notation préfixée, complètement parenthésée.
(define (ebs->string-pol-pref exp)
(cond ((ebs-atomique? exp)
(symbol->string exp))
((ebs-unaire? exp)
(string-append (symbol->string (ebs-unaire-operateur exp))
" "
(ebs->string-pol-pref (ebs-unaire-operande exp))))
((ebs-binaire? exp)
(string-append
(symbol->string (ebs-binaire-operateur exp))
" "
(ebs->string-pol-pref (ebs-binaire-operande-gauche exp))
" "
(ebs->string-pol-pref (ebs-binaire-operande-droit exp))))
(else (erreur 'ebs->string-pol-pref
"expression mal formée"))))
;;; (ebs->string-pol-pref exp) rend la Sexpression représentant exp en
;;; notation préfixée, complètement parenthésée.
(define (ebs->string-pol-pref exp)
(cond ((ebs-atomique? exp)
(symbol->string exp))
((ebs-unaire? exp)
(string-append (symbol->string (ebs-unaire-operateur exp))
" "
(ebs->string-pol-pref (ebs-unaire-operande exp))))
((ebs-binaire? exp)
(string-append
(symbol->string (ebs-binaire-operateur exp))
" "
(ebs->string-pol-pref (ebs-binaire-operande-gauche exp))
" "
(ebs->string-pol-pref (ebs-binaire-operande-droit exp))))
(else (erreur 'ebs->string-pol-pref
"expression mal formée"))))
Fonctions de conversion d'entrée
Considérons, par exemple, la fonction ebs-exp-cste? qui prend comme donnée un élément du type ExprBoolSimple. Si nous voulons faire évaluer une expression d'un langage expBoolSimplea, nous devons avoir une fonction, a->ebs, qui a comme donnée un mot de expBoolSimplea et qui rend une valeur du type ExpBoolSimple (i.e. un élément de la barrière syntaxique des expressions booléennes simples):
;;; a->ebs: a -> ExpBoolSimple
;;; (a->ebs d) rend l'élément de ExpBoolSimple représenté,
;;; dans le langage expBoolSimplea, par «d»
;;; (a->ebs d) rend l'élément de ExpBoolSimple représenté,
;;; dans le langage expBoolSimplea, par «d»
et, pour savoir si l'expression exp-a, écrite dans le langage expBoolSimplea, est une expression constante, il suffit d'écrire:
(ebs-exp-cste? (a->ebs exp-a))
Comme exemples, spécifions et implantons deux convertisseurs d'entrée pour les expressions booléennes simples.
sexpr-pref->ebs
Commençons par le langage préfixe complètement parenthésé. Un mot de ce langage étant complètement parenthésé, il peut être vu comme une Sexpression et le convertisseur d'entrée a donc comme type S-Expression -> ExprBoolSimple. Pour indiquer le type de la donnée et le genre (préfixe) de langage, nous nommerons sexpr-pref->ebs cette fonction dont la spécification est donc:
;;; sexpr-pref->ebs : Sexpression -> ExprBoolSimple
;;; (sexpr-pref->ebs s) rend l'arbre de syntaxe abstraite dont la représentation,
;;; dans le langage exprBoolSimpleprefixe est la Sexpression s
;;; (sexpr-pref->ebs s) rend l'arbre de syntaxe abstraite dont la représentation,
;;; dans le langage exprBoolSimpleprefixe est la Sexpression s
En voici une application:
(ebs-exp-cste? (sexpr-pref->ebs '(@ou (@et a @f) (@non @f))))
Pour implanter cette fonction, on analyse la Sexpression à lire:
-
soit elle est réduite à un symbole (ce n'est pas une liste) et
- soit c'est @v ou @f et il suffit de fabriquer l'expression booléenne représentée par cette constante,
- sinon, c'est une variable et il suffit de fabriquer l'expression booléenne représentée par cette variable,
- soit c'est une Sexpression de longueur 2 et il suffit de
fabriquer l'expression composée unaire dont
- l'opérateur est représenté par le premier élément de la Sexpression donnée,
- l'opérande est obtenue en lisant (appel récursif) le deuxième élément de la Sexpression donnée,
- soit c'est une Sexpression de longueur 3 et il suffit de
fabriquer l'expression composée binaire dont
- l'opérande gauche est obtenue en lisant (appel récursif) le deuxième élément de la Sexpression donnée,
- l'opérateur est représenté par le premier élément de la Sexpression donnée,
- l'opérande droit est obtenue en lisant (appel récursif) le troisième élément de la Sexpression donnée.
D'où l'implantation:
(define (sexpr-pref->ebs s)
(if (pair? s)
(if (pair? (cdr s))
(if (pair? (cddr s))
(if (pair? (cdddr s))
; la liste a au moins 4 éléments:
(erreur 'sexpr-pref->ebs s " mal formée (+4)")
; la liste a 3 éléments:
(ebs-binaire (sexpr-pref->ebs (cadr s))
(sexpr-pref-operateur2 (car s))
(sexpr-pref->ebs (caddr s))))
; la liste a 2 éléments:
(ebs-unaire (sexpr-pref-operateur1 (car s))
(sexpr-pref->ebs (cadr s))))
; la liste a 1 élément:
(erreur 'sexpr-pref->ebs s " mal formée (1)"))
(if (sexpr-pref-constante? s)
(sexpr-pref-constante s)
(sexpr-pref-variable s))))
(if (pair? s)
(if (pair? (cdr s))
(if (pair? (cddr s))
(if (pair? (cdddr s))
; la liste a au moins 4 éléments:
(erreur 'sexpr-pref->ebs s " mal formée (+4)")
; la liste a 3 éléments:
(ebs-binaire (sexpr-pref->ebs (cadr s))
(sexpr-pref-operateur2 (car s))
(sexpr-pref->ebs (caddr s))))
; la liste a 2 éléments:
(ebs-unaire (sexpr-pref-operateur1 (car s))
(sexpr-pref->ebs (cadr s))))
; la liste a 1 élément:
(erreur 'sexpr-pref->ebs s " mal formée (1)"))
(if (sexpr-pref-constante? s)
(sexpr-pref-constante s)
(sexpr-pref-variable s))))
;;; sexpr-pref-constante? : Symbole -> bool
;;; (sexpr-pref-constante? s) rend #t ssi s représente une constante
(define (sexpr-pref-constante? s)
(member s '(@v @f)))
;;; (sexpr-pref-constante? s) rend #t ssi s représente une constante
(define (sexpr-pref-constante? s)
(member s '(@v @f)))
;;; sexpr-pref-constante : Symbole -> ExprBoolSimple
;;; (sexpr-pref-constante s) rend l'expression réduite à la constante
;;; représentée par s
(define (sexpr-pref-constante s)
(cond ((equal? s '@v) (ebs-constante-vrai))
((equal? s '@f) (ebs-constante-faux))
(else (erreur 'sexpr-pref->ebs s "n'est pas une constante"))))
;;; (sexpr-pref-constante s) rend l'expression réduite à la constante
;;; représentée par s
(define (sexpr-pref-constante s)
(cond ((equal? s '@v) (ebs-constante-vrai))
((equal? s '@f) (ebs-constante-faux))
(else (erreur 'sexpr-pref->ebs s "n'est pas une constante"))))
;;; sexpr-pref-variable : Symbole -> ExprBoolSimple
;;; (sexpr-pref-variable s) rend l'expression réduite à la variable
;;; représentée par s
(define (sexpr-pref-variable s)
(ebs-variable s))
;;; (sexpr-pref-variable s) rend l'expression réduite à la variable
;;; représentée par s
(define (sexpr-pref-variable s)
(ebs-variable s))
;;; sexpr-pref-operateur1 : Symbole -> Operateur1
;;; (sexpr-pref-operateur1 s) rend l'opérateur unaire représenté par s
(define (sexpr-pref-operateur1 s)
(if (equal? s '@non)
(ebs-operateur1-non)
(erreur 'sexpr-pref->ebs s "n'est pas un opérateur unaire")))
;;; (sexpr-pref-operateur1 s) rend l'opérateur unaire représenté par s
(define (sexpr-pref-operateur1 s)
(if (equal? s '@non)
(ebs-operateur1-non)
(erreur 'sexpr-pref->ebs s "n'est pas un opérateur unaire")))
;;; sexpr-pref-operateur2 : Symbole -> Operateur2
;;; (sexpr-pref-operateur2 s) rend l'opérateur binaire représenté par s
(define (sexpr-pref-operateur2 s)
(cond ((equal? s '@et) (ebs-operateur2-et))
((equal? s '@ou) (ebs-operateur2-ou))
(else (erreur 'sexpr-pref->ebs s "n'est pas un opérateur binaire"))))
;;; (sexpr-pref-operateur2 s) rend l'opérateur binaire représenté par s
(define (sexpr-pref-operateur2 s)
(cond ((equal? s '@et) (ebs-operateur2-et))
((equal? s '@ou) (ebs-operateur2-ou))
(else (erreur 'sexpr-pref->ebs s "n'est pas un opérateur binaire"))))
polonaise-prefixe->ebs
Donnons la grammaire:
| <expBoolSimplepolonaise> | -> | <atomique> |
| <unaire> | ||
| <binaire> | ||
| <unaire> | -> | <opérateur1> <expBoolSimplepolonaise> |
| <binaire> | -> | <opérateur2> <expBoolSimplepolonaise> <expBoolSimplepolonaise> |
| <atomique> | -> | <constante> |
| <variable> | ||
| <constante> | -> | @f | faux |
| @v | vrai | ||
| <variable> | -> | Une suite de caractères autres que l'espace et les parenthèses |
| <opérateur1> | -> | @non |
| <opérateur2> | -> | @et | et |
| @ou | ou | ||
Exemple: @et @non@ou @f @v @f
Premier problème:
L'écriture d'un convertisseur d'entrée est alors beaucoup moins simple que précédemment. En effet @et @non @ou @f @v @f n'est pas une Sexpression et nous avons vu qu'en Scheme seules les Sexpressions pouvaient être des données.
Il faut donc tricher. Deux solutions:
- entourer la donnée par des parenthèses (car on a alors une liste, cas
particulier d'une Sexpression); l'application du convertisseur
d'entrée est alors
(polonaise-prefixe->ebs '(@et @non @ou @f @v @f))
- considérer la donnée comme une chaîne de caractères (rappelons que les
chaînes de caractères sont des Sexpressions « atomiques »);
l'application du convertisseur
d'entrée est alors
(polonaise-prefixe->ebs "@et @non@ou @f @v @f")
la seconde solution étant celle où l'on triche le moins, mais il semble que la première solution soit plus simple à traiter, aussi regardons cette solution.
Second problème:
Mais il y a un autre problème! Pour analyser la liste (@et @non @ou @f @v @f), il faut la découper (on peut facilement voir qu'il s'agit d'un « binaire ») en
- son opérateur, @et: facile, c'est le car de la liste;
- son premier opérande (@non @ou @f @v): comment faire cela? difficile...
- son second opérande (@f)...
Ainsi, même en trichant au maximum, la convertion d'une expression écrite en polonaise préfixée est très difficile. Aussi nous ne le ferons pas... (bien qu'étant hors programme de ce cours, un convertisseur, ayant comme donnée une chaîne de caractères, est fourni en annexe).
Noter que la conversion des expressions écrites « normalement » est encore plus difficile puisque, en plus du découpage, il faut gérer les priorités des opérateurs. Pour les expressions booléennes, nous vous fournirons un convertisseur des expressions écrites « normalement » (sans vous donner le source car on s'éloigne beaucoup trop du programme de ce cours).


