Nommage de valeurs
Exemple
Nous voudrions écrire une définition de la fonction qui, étant données les longueurs des trois côtés d'un triangle quelconque, rend l'aire de ce triangle. Pour ce faire, on peut consulter un (vieux) bouquin de maths et trouver le théorème suivant:
Théorème: L'aire A d'un triangle quelconque de côtés a, b et c est telle que
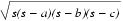 avec s = (a+b+c)/2
avec s = (a+b+c)/2
Théorème que l'on peut aussi écrire:
Théorème: Étant donné un triangle quelconque de côtés a, b et c, en nommant s la valeur (a+b+c)/2, son aire est égale à
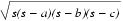
En Scheme, nous écrivons tout simplement:
;;; aire-triangle : Nombre * Nombre * Nombre -> Nombre
;;; (aire-triangle a b c) rend l'aire d'un triangle de cotés «a», «b» et «c»
(define (aire-triangle a b c)
(let ((s (/ (+ a b c ) 2)))
(sqrt (* s (- s a) (- s b) (- s c)))))
;;; (aire-triangle a b c) rend l'aire d'un triangle de cotés «a», «b» et «c»
(define (aire-triangle a b c)
(let ((s (/ (+ a b c ) 2)))
(sqrt (* s (- s a) (- s b) (- s c)))))
;;; TEST pour la fontion aire-triangle (rend 6):
(aire-triangle 3 4 5) -> 6
et nous pourrions paraphraser le corps de cette définition en disant « nommons s la valeur de (/ (+ a b c ) 2); la valeur rendue est (sqrt (* s (- s a) (- s b) (- s c))) ».
Grammaire
L'expression, corps de la définition de aire-triangle est un bloc et elle suit la règle de grammaire:
| <bloc> | -> | (let ( <liaison>* ) <corps> ) |
| <liaison> | -> | ( <variable> <expression> ) |
Ainsi une liaison « attache » à un nom (en Scheme on parle de variable) une valeur, la valeur de l'expression. Une telle liaison est écrite en mettant la variable puis l'expression entre parenthèses.
Dans un bloc, on peut très bien nommer plusieurs valeurs: on aura tout simplement plusieurs liaisons. Ces différentes liaisons doivent elles-mêmes être mises entre parenthèses.
(let ((v1 exp1)
(v2 exp2) )
corps )
(v2 exp2) )
corps )
(define (aire-triangle a b c)
(let ((s (/ (+ a b c ) 2)))
(sqrt (* s (- s a) (- s b) (- s c)))))
(let ((s (/ (+ a b c ) 2)))
(sqrt (* s (- s a) (- s b) (- s c)))))
Exemple récapitulatif
Pour finir cette section, traitons un exemple qui utilise toutes les constructions Scheme que nous avons vues.
Le problème est d'écrire la définition d'une fonction qui calcule le nombre de racines d'une équation du second degré. Par exemple:
| (nombre-racines 3 2 -3) | --> | 2 | (D = 22 +4×3×3 = 40) |
| (nombre-racines 3 2 3) | --> | 0 | (D = 22 -4× 3× 3= -32) |
| (nombre-racines 1 2 1) | --> | 1 | (D =22 -4× 1 × 1 = 0) |
L'algorithme est bien connu: étant donné une équation du second degré, ax2+bx+c, on pose D = b2 - 4ac et, selon que D est négatif, nul ou positif, le nombre de racines est respectivement 0, 1 ou 2. Voici une définition de la fonction:
;;; nombre-racines : Nombre * Nombre * Nombre -> nat
;;; (nombre-racines a b c) rend le nombre de racines de l'équation
;;; « a.x**2 + b.x + c = 0 »
(define (nombre-racines a b c)
(let ((delta (- (* b b) (* 4 a c))))
(if (< delta 0)
0
(if (= delta 0)
1
2))))
;;; (nombre-racines a b c) rend le nombre de racines de l'équation
;;; « a.x**2 + b.x + c = 0 »
(define (nombre-racines a b c)
(let ((delta (- (* b b) (* 4 a c))))
(if (< delta 0)
0
(if (= delta 0)
1
2))))
| Pour s'auto-évaluer |
|---|
|
|
|
|
|
|


