Un n-uplet est une structure de données qui comporte n éléments, le premier étant d'un certain type (toujours le même, par exemple alpha), le deuxième d'un autre type (toujours le même, par exemple beta), le troisième d'un autre type (toujours le même, par exemple gamma)... Nous noterons NUPLET[alpha beta gamma ...] le type de tels n-uplets.
 
On peut dire aussi qu'un n-uplet est un enregistrement, constitué de n champs, chacun étant d'un type bien défini.
 
Par exemple, on peut définir le type  
NUPLET[nat string bool]  

 
qui pourrait correspondre à un enregistrement regroupant différents noms équivalents pour une valeur booléenne et qui comporte trois champs,

• le premier -- que l'on pourrait nommer naturel -- étant de type nat,
• le deuxième -- que l'on pourrait nommer chaine -- étant de type string,
• le troisième -- que l'on pourrait nommer booleen -- étant de type bool.

 
Attention: ne pas confondre LISTE et NUPLET:

• en ce qui concerne l'utilisation:
  • les listes correspondent aux séquences finies,
  • les n-uplets correspondent à des enregistrements;
   
  
• pour le nombre d'éléments:
  • deux listes de type LISTE[a] peuvent avoir des nombres d'éléments différents,
  • deux n-uplets de type NUPLET[...] ont exactement le même nombre d'éléments;
   
  
• pour le type des éléments:
  • tous les éléments d'une liste de type LISTE[a] sont de même type (à savoir a),
  • les différents éléments d'un n-uplet de type NUPLET[...] peuvent être de types différents (et sont, en général, de types différents).
   
  

 
Fonctions de base pour les n-uplets  
Constructeur  
On doit pouvoir « fabriquer » un n-uplet. Par exemple, pour le type NUPLET[nat string bool], on définit la fonction construction telle que, par exemple:  
-> (1 true #t)  

 
Cette fonction peut être définie en utilisant la primitive list:  
 

 
Accesseurs  
On doit pouvoir « accéder » à chacun des éléments (ou « extraire » la valeur d'un champ) d'un n-uplet. Ainsi, pour le type NUPLET[nat string bool], on définit trois fonctions qui extraient respectivement le premier, le deuxième et le troisième éléments.
 
Par exemple, si noms-vrai est l'élément égal à (construction 1 "true" #t):

• pour le premier élément:
   
  (extraction-naturel noms-vrai) -> 1  
  
• pour le deuxième élément:
   
  (extraction-chaine noms-vrai) -> "true"  
  
   
  
• pour le troisième élément:
   
  (extraction-booleen noms-vrai) -> #T  
  

 
Les définitions de ces fonctions d'extraction s'écrivent facilement à l'aide des fonctions car et cdr (et des abréviations cadr, caddr...):

• pour le premier élément:
   
  
  ;;; extraction-naturel : NUPLET[nat string bool] -> nat 
  ;;; (extraction-naturel t) rend «a» lorsque «t» est le triplet «(a b c)» 
  (define (extraction-naturel t)
    (car t))
   
  
• pour le deuxième élément:
   
  
  ;;; extraction-chaine : NUPLET[nat string bool] -> string 
  ;;; (extraction-chaine t) rend «b» lorsque «t» est le triplet «(a b c)» 
  (define (extraction-chaine t)
    (cadr t))
   
  

 

• et, enfin, pour le troisième élément:
   
  
  ;;; extraction-booleen : NUPLET[nat string bool] -> bool 
  ;;; (extraction-booleen t) rend «c» lorsque «t» est le triplet «(a b c)» 
  (define (extraction-booleen t)
    (caddr t))
   
  

 
Pour extraire le i+1^eme, on utilise la fonction cadⁱr, dⁱ exprimant que l'on écrit i fois la lettre d.
 
Remarque: classiquement,

• la fonction de construction est souvent nommée par le nom du type de l'élément que l'on construit (dans l'exemple précédent, puisqu'un n-uplet correspond à un enregistrement regroupant différents noms équivalents pour une valeur booléenne, la fonction construction serait ainsi nommée noms-valeur-booleenne),
• les fonctions d'extraction sont souvent nommées par le nom du champ de l'élément que l'on extrait (dans l'exemple précédent, la fonction extraction-naturel serait ainsi nommée naturel).

 
Ainsi, les définitions des différentes fonctions seraient:  

 

 

 

 
 

 
Notion de niveaux d'abstraction (premier regard)  
On peut remarquer que nous avons implanté les types LISTE[a] et NUPLET[a] en utilisant dans les deux cas les fonctions list, car et cdr. Ceci peut prêter à confusion et c'est pourquoi, dès le début, nous avons insisté sur les différences entre ces deux types.
 
En fait, les notions de LISTE et de NUPLET n'existent pas dans Scheme. C'est nous qui les définissons dans le cadre de ce cours et qui les utilisons. Mais travaillant en Scheme, nous devons implanter ces notions en Scheme et, pour ce faire, nous avons utilisé la même structure de données Scheme, à savoir la « structure de liste » (qui n'est pas équivalente à notre notion de LISTE).
 
Mais nous aurions pu aussi utiliser d'autres structures de données Scheme pour implanter ces types (nous verrons, lors de la troisième saison, une autre implantation des NUPLET). Ainsi, lorsque nous parlons de LISTE ou de NUPLET, nous sommes à un niveau d'abstraction plus élevé.
 
Plus concrètement, supposons que, dans l'écriture d'un programme, nous ayons besoin de manipuler des noms de valeurs booléennes, triplets de valeurs de types ánat, string, boolñ et, pour ce faire, nous avons vu que nous avions besoin du constructeur et des accesseurs naturel, booleen et chaine. Nous pouvons représenter ce besoin par le schéma suivant où la flèche indique que l'« on se sert de »:  
 

 
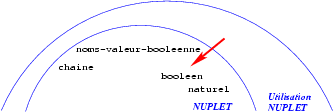
Mais ces fonctions n'existent pas en Scheme. Aussi nous les implantons, en utilisant une certaine structure de données Scheme, sans avoir besoin de nous préoccuper de leur utilisation:  
 

 
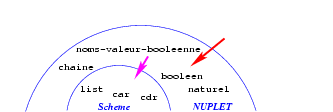
En fusionnant les schémas des deux phases, nous obtenons:  
 

 
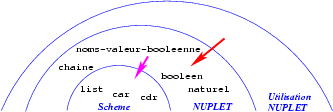
schéma qui montre bien les différents niveaux auquels on peut se placer, niveaux dans lesquels la notion de n-uplet est de plus en plus abstraite lorsque l'on s'éloigne du centre des demi-cercles.
 
À noter:

1. Nous avons déjà dit que l'on pouvait implanter les n-uplets à l'aide d'autres structures de données Scheme. Aussi -- pour faciliter l'évolution du logiciel -- est-il recommandé, au niveau de l'utilisation des NUPLET, de ne pas utiliser la connaissance que l'on a de l'implantation retenue. C'est pourquoi, dans notre schéma, il n'y a pas de flèche allant du niveau le plus élevé (« utilisation NUPLET ») au niveau le moins élevé (« Scheme »). Pour insister sur ce point, très important en génie logiciel, on parle de barrière d'abstraction. Nous reverrons cette notion de nombreuses fois par la suite.
2. Dans les problèmes -- simples -- que nous traiterons cette saison, nous ne définirons pas systématiquement les fonctions du niveau d'abstraction « NUPLET » (et nous utiliserons donc les fonctions car, cdr... au niveau d'abstraction « utilisation NUPLET »), mais, systématiquement, nous raisonnerons en terme de n-uplets.