Premier exemple d'une définition récursive sur les listes  
Écrivons une définition de la fonction longueur qui rend la longueur d'une liste donnée:  
(longueur (list 3 5 2 5)) -> 4
 
(longueur (list)) -> 0
 
(longueur (list 3)) -> 1
 
(longueur (list 3 5)) -> 2  

• lorsque la liste n'est pas vide, sa longueur est égale à 1 plus la longueur de la liste « qui reste »;
• la longueur de la liste vide est 0.

 
D'où le source Scheme:
 
 

 
Dans la définition précédente, pour définir la fonction longueur, nous utilisons cette même fonction: cette définition est donc récursive.
 
Vous pouvez regarder comment DrScheme évalue (longueur (list 3 5)) en lui demandant d'évaluer cette expression en « pas à pas » (icone « Step »).
 
En utilisant la fonction longueur, on peut donner une nouvelle définition de la fonction lg>1? vue précédemment:  
 

 
Cette définition paraît meilleure (elle est plus simple) que la définition donnée précédemment. Elle est à proscrire car elle est beaucoup moins efficace:

• avec la première définition, une évaluation de (lg>1? L) applique la fonction pair? au plus deux fois,
• avec la seconde définition, si n est la longeur de la liste L, l'évaluation de (lg>1? L) applique la fonction pair? n+1 fois.

 
Remarque: de fait cette fonction est une primitive de Scheme (et elle se nomme length). Dans la suite du cours, nous redéfinirons d'autres primitives (car ce sont des exemples intéressants et parce que, pour évaluer l'efficacité des algorithmes, il faut savoir comment elles sont implantées), mais en les nommant alors avec le mot anglais (nous n'avons pas pu le faire ici car nous voulions faire du pas à pas).
 
Schéma de récursion (simple) sur les listes  
La définition de la notion de liste étant récursive, il n'est pas étonnant que la plupart des définitions de fonctions sur les listes soient des définitions récursives. Le schéma récursif fondamental sur les listes est semblable à la définition récursive des listes: on commence par traiter le cas général d'une liste non vide (appel récursif sur le reste de la liste et combinaison du résultat avec le premier de ses éléments), puis l'on traite le cas de base (la liste vide).
 
 

 
où base est la valeur à rendre lorsque la liste est vide, et combinaison est la fonction combinant le résultat de l'appel récursif avec le premier élément de la liste. Ainsi, pour la fonction longueur (la combinaison n'utilise pas (car L)):
 
 

Schéma	longueur
base	0
(combinaison (car L) (fonction (cdr L)))	(+ 1 (longueur (cdr L)))

 
Exemples de définitions récursives  
Exemple 1: écrivons une définition de la fonction somme qui rend la somme des éléments d'une liste de nombres donnée:
 
(somme (list 2 5 7)) -> 14
 
(somme (list)) -> 0  

• lorsque la liste donnée n'est pas vide, la somme de ses éléments est égale à la valeur de son premier élément plus la somme des éléments du cdr de la liste (combinaison º +);
• la somme des éléments d'une liste vide est 0 (base º 0):

 
 
 

 
Exemple 2: écrivons une définition de la fonction conc-d qui ajoute un élément à la fin d'une liste:
 
(conc-d (list 1 2 3) 4) -> (1 2 3 4)
 
(conc-d (list) 1) -> (1)  

• combinaison º cons,
• base º (list x):

 
 
 

 
Exemple 3: écrivons une définition de la fonction append qui concatène (met « bout à bout ») deux listes données. Par exemple:
 
(append (list 1 2) (list 3 4 5)) -> (1 2 3 4 5)  

 
Il suffit de faire une récursion sur la première liste comme le montre le dessin suivant:
 
 

 

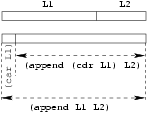
• combinaison º cons,
• base º L2:

 
 
 

 
Retour sur la méthode de travail pour écrire des définitions récursives  
Exemple  
Nous voudrions écrire la fonction eme telle que  
(eme 3 (list 1 2 5 3 4 3 4)) -> 4
 
(eme 3 (list 1 2)) -> 0

 
(eme a L) rend l'entier p défini comme suit: si a est égal au premier élément de la liste L, p est égal à 1, sinon, si a est égal au deuxième élément de liste, p est égal à 2... et si a n'a pas d'occurrence dans L, p est égal à 0.
 
Idée: en général, si a est égal à (car L), eme(a, L) est égal à 1 et, sinon, eme(a, L) est égal à 1 + eme(a, (cdr L)) et il faut « enlever » la liste vide:
 

 

 
Bien sûr, vu ce qui est écrit, le programme est faux. En effet, si on l'essaie:
 
(eme-faux 3 (list 1 2 5 3 4 3 4)) -> 4
 
(eme-faux 3 (list 1 2)) -> 2

 
Que c'est-il passé?
 
En fait, dans la spécification, le cas où a n'a pas d'occurrence dans L est un cas particulier et, dans ce cas, notre égalité est fausse (encore une « démonstration » de 1 + 0 = 0!) et nous devons donc le traiter comme un cas particulier. Comment reconnait-on ce cas particulier? c'est que le résultat est nul:
 

 

 
Méthode de travail  
Nous rappelons la méthode de travail pour l'écriture de définitions récursives en ajoutant, par rapport à ce qui a été donné précédemment, le problème des cas particuliers dans la spécification.
 
Pour écrire une définition récursive, on doit suivre la méthode suivante:

1. Décomposer la donnée (x étant la donnée, d₁(x)... sont des éléments de X « plus petits » que x).
2. Écrire la relation de récurrence, c'est-à-dire une égalité qui est vraie (presque toujours) entre f(x) et une expression (dite de récurrence) qui contient des occurrences de f(d_i(x)).
3. Déterminer les valeurs (« de base ») pour lesquelles:
   1. l'égalité est fausse; en particulier,
      • regarder quand l'expression de récurrence n'est pas définie et
      • regarder les valeurs (de x et de d_i(x)) où l'une des fonctions utilisées (la fonction à implanter et les autres fonctions intervenant dans l'expression de récurrence) est définie par un cas particulier;
   2. les valeurs d_i(x) ne sont pas strictement « plus petites » que x; en particulier, regarder si d_i(x) peut être égal à x.
4. Déterminer la valeur de la fonction f pour les valeurs de base.

 
Remarque: lorsque la spécification d'une fonction comporte des cas particuliers, il faut en tenir compte, non seulement lors de l'implantation de la fonction, mais aussi lors de toute implantation -- de n'importe quelle fonction -- qui utilise cette fonction (cf. le cas i) du cas c) de la méthode donnée ci-dessus). Bien évidemment cela est une source importante d'erreurs: il faut éviter le plus possible d'avoir des cas particuliers dans la spécification des fonctions!
 
Efficacité et nommage de valeurs  
La définition donnée pour la fonction eme-0 est très, très mauvaise. Elle est juste (la fonction rend bien ce que l'on attend d'elle, mais elle est inacceptable! En effet, dans l'expression définissant la fonction, nous calculons deux fois (eme-0 a (cdr L)). Dans notre idée, il suffisait de parcourir tous les éléments de la liste, le temps est donc de l'ordre de n, si n est le nombre d'éléments de la liste donnée. Or, avec la définition que nous avons donné, pour calculer (eme-0 L), il faut donc un peu plus que deux fois le temps pour calculer (eme-0 a (cdr L)). Si L a n éléments, (cdr L) a n-1 éléments: en nommant t_n le temps de calcul de l'application de la fonction à une liste de n éléments, t_n est plus grand que 2× t_n-1. t_n est donc au moins de l'ordre de 2ⁿ: dès que la liste sera un peu longue, le temps de calcul sera prohébitif et personne n'aura le courage d'attendre le résultat!
 
Oui, mais, on a besoin à deux endroits de la valeur de (eme-0 a (cdr L)). Pour n'évaluer qu'une fois cette application, il faut nommer sa valeur (à l'aide d'un let):
 
 

 
Noter que l'on doit écrire le bloc dans l'alternant de l'alternative car, avant, (cdr L) peut ne pas être définie (lorsque L est vide).