Les arbres binaires sont des structures de données très utiles en informatique. Dans cette section, comme exemple d'utilisation des arbres binaires, nous étudions les « arbres binaires de recherche ».
 
Introduction et définition  
En informatique, il est fréquent d'avoir besoin de gérer un ensemble d'informations (comme l'ensemble des étudiants de DEUG-MIAS). Dans cette gestion, l'une des opérations fondamentales est de savoir si un individu donné (connu par son nom ou par son numéro de carte d'étudiant) fait, ou ne fait pas, partie de la base. Pour ce faire, il existe une structure de données efficace, la structure d'arbre binaire de recherche.
 
Un arbre binaire de recherche est un arbre binaire vide ou un arbre binaire qui possède les propriétés suivantes:

• l'étiquette de sa racine est
  • supérieure à toutes les étiquettes de son sous-arbre gauche,
  • inférieure à toutes les étiquettes de son sous-arbre droit,
   
  
• ses sous-arbres gauche et droit sont aussi des arbres binaires de recherche.

 
Par la suite, pour que les opérations de comparaison soient définies (et soient < et >), nous considèrerons que les étiquettes sont des nombres.
 
Voici un exemple d'arbre binaire de recherche:
 
 

 
Les propriétés caractéristiques de la notion d'arbre binaire de recherche sont intéressantes pour l'efficacité de la recherche car elles permettent de ne chercher un élément que dans un des deux sous-arbres, recherche qui s'effectue en ne recherchant que dans un des deux sous-sous-arbres...
 
Notons que, dans un arbre binaire de recherche, c'est l'ensemble de ses étiquettes qui nous intéresse: deux arbres binaires de recherche peuvent donc être « équivalents ». Par exemple, en tant qu'arbres binaires de recherche, l'arbre précédent est « équivalent » à l'arbre suivant:
 
 

 
Spécification  
Nous nommerons ArbreBinRecherche le type des arbres binaires de recherche, et, par la suite, nous voudrions définir les fonctions suivantes:
 
 

 
Par exemple, dans notre implantation, si abr1 est l'arbre binaire de recherche dessiné ci-dessus, (abr-recherche 5 abr1) a comme valeur  
 

 
 

 
Par exemple, dans notre implantation -- et une autre implantation peut rendre un arbre binaire de recherche équivalent --, (abr-ajout 17 abr1) a comme valeur
 
 
 

 
Par exemple, dans notre implantation -- et une autre implantation peut rendre un arbre binaire de recherche équivalent --, (abr-moins 10 abr1) a comme valeur
 
 
Noter que lorsque l'élément à supprimer est l'étiquette d'un noeud interne, obligatoirement, l'arbre binaire est profondemment modifié.
 
Implantation  
Naturellement, nous implantons les arbres binaires de recherche à l'aide de la barrière d'abstraction ArbreBinaire.
 
Fonction abr-recherche  
Rappelons la spécification:
 
 

 
L'idée (récursive) de l'implantation est très simple:

• lorsque l'élément recherché est égal à l'étiquette de la racine, on l'a trouvé et le résultat est l'arbre lui-même;
• sinon, on doit rechercher l'élément dans le sous-arbre gauche ou dans le sous-arbre droit suivant qu'il est inférieur ou supérieur à l'étiquette de la racine.

 
D'où la définition:
 
 

 
Fonction abr-ajout  
Rappelons la spécification:
 
 

 
L'idée (récursive) de l'implantation est également très simple:

• lorsque l'élément à ajouter est égal à l'étiquette de la racine, le résultat est l'arbre donné;
• lorsque l'élément à ajouter est inférieur à l'étiquette de la racine, il doit être dans le sous-arbre gauche, aussi le résultat est l'arbre
  • dont l'étiquette est l'étiquette de l'arbre donné,
  • dont le sous-arbre gauche est l'arbre obtenu en ajoutant l'élément dans le sous-arbre gauche de l'arbre donné,
  • dont le sous-arbre droit est le sous-arbre droit de l'arbre donné;
   
  
• lorsque l'élément à ajouter est supérieur à l'étiquette de la racine, il doit être dans le sous-arbre droit et on raisonne comme ci-dessus en inversant sous-arbre gauche et sous-arbre droit.

 
D'où la définition:
 
 

 
Remarque: le recueil d'exercices contient une autre implantation de cette fonction.
 
Fonction abr-moins  
Rappelons la spécification:
 
 

 
L'idée initiale est encore très simple (mais ça se complique par la suite...):

• lorsque l'élément à supprimer est inférieur à l'étiquette de la racine, cet élément ne peut être que dans le sous-arbre gauche, et le résultat est donc l'arbre
  • dont l'étiquette est l'étiquette de l'arbre donné,
  • dont le sous-arbre gauche est l'arbre obtenu en supprimant l'élément du sous-arbre gauche de l'arbre donné,
  • dont le sous-arbre droit est le sous-arbre droit de l'arbre donné;
   
  
• lorsque l'élément à supprimer est supérieur à l'étiquette de la racine, cet élément ne peut être que dans le sous-arbre droit, et on raisonne comme ci-dessus en inversant sous-arbre gauche et sous-arbre droit;
• reste le cas où l'élément à supprimer est égal à l'étiquette de la racine; il faut le supprimer, mais on doit alors complètement reconstruire l'arbre, et de tel sorte que cet arbre vérifie la propriété « être un arbre binaire de recherche »; compliqué... comme d'habitude, dans ce cas, on utilise et spécifie une nouvelle fonction:

 
 
 

 
La spécification de moins-racine étant:
 
 

 
Comment implanter cette fonction?
 
Première idée:
 
 

 
Seconde idée:
 
Deux situations entraînent une solution évidente: lorsque l'un des deux sous-arbres est vide, le résultat est l'autre sous-arbre. Dans le cas contraire, on peut essayer de « conserver » un des deux sous-arbres, le droit par exemple: pour obtenir un arbre qui vérifie la propriété « arbre binaire de recherche », il faut alors que la racine de l'arbre résultat soit le plus grand élément du sous-arbre gauche. Ainsi, le résultat est un arbre

• ayant comme racine le plus grand élément du sous-arbre gauche de l'arbre donné (noter que c'est celui qui est au bout de la branche la plus à droite de ce sous-arbre gauche),
• ayant comme sous-arbre gauche, le sous-arbre gauche de l'arbre donné privé de son plus grand élément,
• ayant comme sous-arbre droit, le sous-arbre droit de l'arbre donné:

 
 
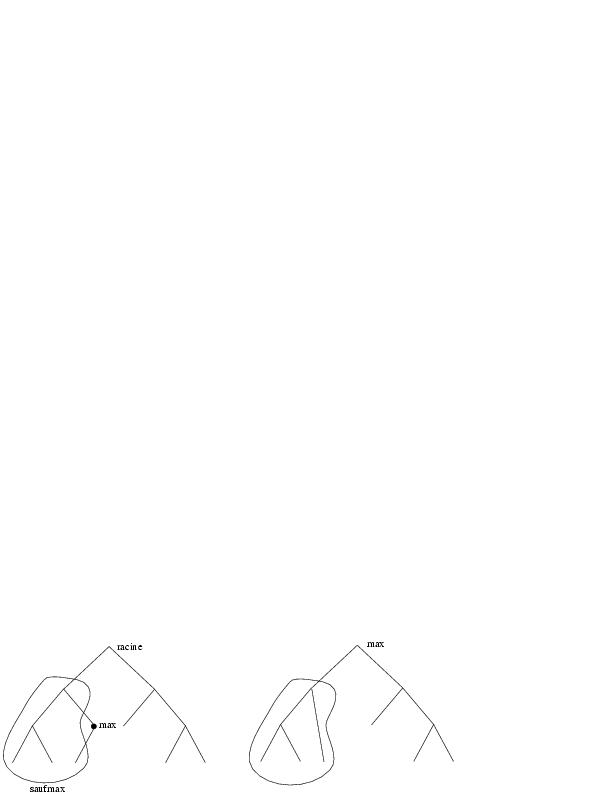
Ainsi, pour implanter la fonction moins-racine, on a besoin de la fonction max-sauf-max de spécification:
 
 

 
La définition de la fonction moins-racine étant alors:
 
 

 
Ne reste plus qu'à implanter la fonction max-sauf-max. Comme nous l'avons noté, le plus grand des éléments présents dans un arbre binaire de recherche se trouve au bout de la branche la plus à droite de cet arbre. Ainsi, la recherche du maximum et la constitution de l'arbre privé de son maximum s'effectuent par l'exploration successive des sous-arbres droits: