Barrière d'abstraction des arbres binaires

Caractéristiques des arbres binaires
Parmi la famille des arbres, les arbres binaires sont caractérisés par:

information attachée à chaque noeud,
existence de l'arbre vide,
chaque noeud a exactement deux sous-arbres immédiats.

Barrière d'abstraction des arbres binaires
Notation: lorsque le type des étiquettes attachées aux noeuds est a, on notera ArbreBinaire[a] le type des arbres binaires.

Dans ce paragraphe, nous donnons la spécification de la barrière d'abstraction des arbres binaires. Nous vous montrerons une implantation de cette barrière plus tard. Pour que vous puissiez l'utiliser avant de voir cette implantation, nous vous fournissons une autre implantation que vous pouvez utiliser, en TME ou chez vous, sous réserve d'avoir chargé « miastools.plt » (cf. installation du céderom).

Dans la bibiothèque MIAS de DrScheme, la barrière d'abstraction des arbres binaires comporte l'ensemble des fonctions (constructeurs, reconnaisseurs et accesseurs) suivantes:

Constructeurs

;;; ab-vide : -> ArbreBinaire[a] ;;; (ab-vide) rend l'arbre binaire vide.

;;; ab-noeud : a * ArbreBinaire[a] * ArbreBinaire[a] -> ArbreBinaire[a] ;;; (ab-noeud e B1 B2) rend l'arbre binaire formé de la racine d'étiquette ;;; «e», du sous-arbre gauche «B1» et du sous-arbre droit «B2».

Exemples

Pour construire l'arbre suivant:

on peut écrire:

(ab-noeud '+ (ab-noeud 3 (ab-vide) (ab-vide)) (ab-vide))

On ne sait rien de la représentation des arbres ainsi construits. Autrement dit, si vous utilisez l'implantation fournie et si vous tapez une telle expression -- toute seule, sans être un argument d'une application --, son évaluation affiche #<abstract:AB> qui indique que le résultat est un arbre binaire mais qu'il est manipulé au niveau abstrait, c'est-à-dire que l'on ne veut pas montrer son implantation.

Ainsi, on peut tester les fonctions dont la donnée est un arbre binaire. Pour tester des fonctions dont le résultat est un arbre binaire, la barrière d'abstraction contient une fonction supplémentaire, la fonction ab-expression, qui a comme spécification:

;;; ab-expression: ArbreBinaire[a] -> Sexpression ;;; (ab-expression B) rend une Sexpression reflétant la construction de l'arbre binaire «B».

Autrement dit, cette fonction rend une expression Scheme qui permet de construire (en utilisant les deux constructeurs) l'arbre donné. Par exemple l'application:

(ab-expression (ab-noeud '+ (ab-noeud 3 (ab-vide) (ab-vide)) (ab-vide)))

a comme valeur

(ab-noeud '+ (ab-noeud 3 (ab-vide) (ab-vide)) (ab-vide))

(le résultat est bien l'expression donnée comme argument à la fonction ab-expression).

Pour construire des arbres binaires, il est très pratique d'avoir aussi à disposition la fonction ab-feuille de spécification:

;;; ab-feuille : a -> ArbreBinaire[a] ;;; (ab-feuille e) rend l'arbre binaire constitué d'une feuille, ayant «e» comme étiquette

Sa définition peut être:

(define (ab-feuille e) (ab-noeud e (ab-vide) (ab-vide)))

Voici un exemple d'application:

(ab-expression (ab-noeud '+ (ab-feuille 3) (ab-vide)))

a comme valeur

(ab-noeud '+ (ab-noeud 3 (ab-vide) (ab-vide)) (ab-vide))

La barrière d'abstraction comporte aussi des reconnaisseurs et des accesseurs:

Reconnaisseurs

;;; ab-noeud? : ArbreBinaire[a] -> bool ;;; (ab-noeud? B) rend vrai ssi «B» n'est pas l'arbre vide.

;;; ab-vide? : ArbreBinaire[a] -> bool ;;; (ab-vide? B) rend vrai ssi «B» est l'arbre vide.

Accesseurs

;;; ab-etiquette : ArbreBinaire[a] -> a ;;; (ab-etiquette B) rend l'étiquette de la racine de l'arbre «B» ;;; ERREUR lorsque «B» ne satisfait pas «ab-noeud?»

;;; ab-gauche : ArbreBinaire[a] -> ArbreBinaire[a] ;;; (ab-gauche B) rend le sous-arbre gauche de «B» ;;; ERREUR lorsque «B» ne satisfait pas «ab-noeud?»

;;; ab-droit : ArbreBinaire[a] -> ArbreBinaire[a] ;;; (ab-droit B) rend le sous-arbre droit de «B» ;;; ERREUR lorsque «B» ne satisfait pas «ab-noeud?»

Propriétés remarquables
Les fonctions de la barrière d'abstraction des arbres binaires vérifient les propriétés suivantes:

Pour tout couple d'arbres binaires, G et D, et toute valeur, v:

(ab-etiquette (ab-noeud v G D)) -> v (ab-gauche (ab-noeud v G D)) -> G (ab-droit (ab-noeud v G D)) -> D

Pour tout arbre binaire non vide B

(ab-noeud (ab-etiquette B) (ab-gauche B) (ab-gauche B)) -> B

Exemples d'utilisations de la barrière d'abstraction
Pour commencer, on peut définir la fonction ab-feuille? dont la spécification est:

;;; ab-feuille? : ArbreBinaire[a] -> bool ;;; (ab-feuille? B) rend #t ssi «B» est un arbre binaire réduit à une feuille ;;; ERREUR lorsque l'arbre est vide

Sa définition peut être:

(define (ab-feuille? B) (and (ab-vide? (ab-gauche B)) (ab-vide? (ab-droit B))))

et alors

(ab-feuille? (ab-feuille 3))

a comme valeur #t
et

(ab-feuille? (ab-noeud '+ (ab-feuille 3) (ab-vide)))

a comme valeur #f
Profondeur d'un arbre
On définit récursivement la profondeur d'un arbre binaire comme suit :

la profondeur de l'arbre vide est 0,
la profondeur d'un arbre non vide est égale au maximum des profondeurs de ses sous-arbres immédiats, augmenté de 1.

Par exemple, la profondeur de l'arbre

est égale à 2.

Pour écrire une définition de la fonction ab-profondeur:

;;; ab-profondeur : ArbreBinaire[a] -> nat ;;; (ab-profondeur B) rend la profondeur de l'arbre «B»

il suffit de suivre la définition mathématique de la fonction:

(define (ab-profondeur B) (if (ab-vide? B) 0 (+ 1 (max (ab-profondeur (ab-gauche B)) (ab-profondeur (ab-droit B))))))

Liste infixe des étiquettes d'un arbre
La liste infixe des étiquettes d'un arbre binaire est définie comme suit:

si B est l'arbre vide alors sa liste infixe est vide,
sinon, la liste infixe de B est égale à la concaténation de la liste infixe du sous-arbre gauche de B suivi de l'étiquette de la racine de B et de la liste infixe du sous-arbre droit de B.

Par exemple, la liste infixe de l'arbre

est égale à (c b d a e).
Pour écrire une définition de la fonction

;;; ab-liste-infixe : ArbreBinaire[a] -> LISTE[a] ;;; (ab-liste-infixe B) rend la liste infixe des étiquettes de l'arbre «B»

il suffit de suivre la définition mathématique de la fonction:

(define (ab-liste-infixe B) (if (ab-vide? B) '() (append (ab-liste-infixe (ab-gauche B)) (cons (ab-etiquette B) (ab-liste-infixe (ab-droit B))))))

Affichage d'un arbre
Dans ce paragraphe, nous étudions la fonction ab-affichage qui permet un affichage plus visuel que la fonction ab-expression: B étant un arbre binaire, (ab-affichage B) rend un paragraphe tel que

si B est l'arbre vide, le paragraphe résultat est composé d'une seule ligne, la ligne vide;
sinon, le paragraphe résultat est composé
- d'une ligne qui contient l'étiquette de l'arbre,
- les lignes suivantes contiennent la représentation présentement définie du sous-arbre gauche, chaque ligne étant préfixé par le caractère tiret (« - »),
- les lignes suivantes contiennent la représentation présentement définie du sous-arbre droit, chaque ligne étant également préfixé par le caractère tiret (« - »).

Ainsi, si ex-ab-2 est l'arbre

(ab-affichage ex-ab-2) a comme valeur

" a -b --c ---vide ---vide --d ---vide ---vide -e --vide --vide "

Spécification

;;; ab-affichage : ArbreBinaire[a] -> Paragraphe ;;; (ab-affichage B) rend, lorsque «B» est l'arbre vide, le paragraphe constitué de la ;;; seule ligne constituée par le mot qui s'affiche "vide" et, lorsque l'arbre «B» n'est pas ;;; vide, le paragraphe dont la première ligne est l'étiquette de la racine de l'arbre «B» ;;; et dont les lignes suivantes sont égales à cette représentation des deux ;;; sous-arbres de «B», toutes les lignes étant préfixées par un tiret

Première implantation

Idée

Considérons l'exemple précédent:

La première ligne est la représentation de l'étiquette de la racine et les lignes suivantes correspondent à la représentation du sous-arbre gauche et du sous-arbre droit, chaque ligne étant précédée d'un tiret:

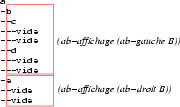
Définition de la fonction

Ainsi, pour implanter la fonction, il suffit:

à partir de la représentation des sous-arbres gauche et droit (appel récursif),
de « fabriquer » la liste des lignes de ces deux représentations (en utilisant les fonctions lignes et append),
de « maper » une fonction qui ajoute un tiret en tête de ligne sur cette liste de lignes,
de concaténer la représentation de l'étiquette de la racine de l'arbre donné devant le paragraphe correspondant à la liste obtenue.

Cette expression n'étant pas définie lorsque l'arbre est vide, la définition de la fonction est:

(define (ab-affichage B) ;; add-tiret-prefixe : Ligne -> Ligne ;; (add-tiret-prefixe ligne) rend la ligne obtenue en ajoutant un tiret devant «ligne» (define (add-tiret-prefixe ligne) (string-append "-" ligne)) ;; expression de (ab-affichage B): (if (ab-vide? B) (paragraphe '("vide")) (paragraphe-cons (->string (ab-etiquette B)) (paragraphe (map add-tiret-prefixe (append (lignes (ab-affichage (ab-gauche B))) (lignes (ab-affichage (ab-droit B)))))))))

Seconde implantation

Avec la définition précédente, l'évaluation de la fonction ab-affichage passe son temps à fabriquer un paragraphe à partir d'une liste de lignes (en utilisant la fonction paragraphe) et à refabriquer la liste de lignes à partir de ce paragraphe (en utilisant la fonction lignes. Pour éviter cela, on peut définir une fonction auxiliaire, liste-lignes-affichage, qui rend la liste des lignes du paragraphe recherché:

;;; ab-affichage : ArbreBinaire[a] -> Paragraphe ;;; (ab-affichage B) rend, lorsque «B» est l'arbre vide, le paragraphe constitué de la ;;; seule ligne constituée par le mot qui s'affiche "vide" et, lorsque l'arbre «B» n'est pas ;;; vide, le paragraphe dont la première ligne est l'étiquette de la racine de l'arbre «B» ;;; et dont les lignes suivantes sont égales à cette représentation des deux ;;; sous-arbres de «B», toutes les lignes étant préfixées par un tiret (define (ab-affichage B) ;; add-tiret-prefixe : Ligne -> Ligne ;; (add-tiret-prefixe ligne) rend la ligne obtenue en ajoutant un tiret devant «ligne» (define (add-tiret-prefixe ligne) (string-append "-" ligne)) ;; liste-lignes-affichage : ArbreBinaire[a] -> LISTE[Ligne] ;; (liste-lignes-affichage B) rend (lignes (ab-affichage B)) (define (liste-lignes-affichage B) (if (ab-vide? B) '("vide") (cons (->string (ab-etiquette B)) (map add-tiret-prefixe (append (liste-lignes-affichage (ab-gauche B)) (liste-lignes-affichage (ab-droit B))))) ) ) ;; expression de (ab-affichage B): (paragraphe (liste-lignes-affichage B)) )

Troisième implantation

Pour avoir une définition plus efficace¹ de cette fonction, on peut aussi utiliser la technique que nous avons expliquée lorsque nous avons écrit la définition de la fonction triangle2: on définit une fonction interne qui rend un paragraphe obtenu en préfixant l'affichage d'un arbre donné par un préfixe donné et on applique cette fonction avec un préfixe vide et l'arbre donné:

(define (ab-affichage B) ;; aff-Aux : Ligne * ArbreBinaire[a] -> LISTE[Ligne] ;; (aff-Aux pref B) rend la liste de lignes obtenue en préfixant chaque ligne de ;; (lignes (ab-affichage B)) par la chaîne «pref» ... à faire ... à faire ... à faire ... à faire ... à faire ... à faire ... à faire ;; expression de (ab-affichage B) : (paragraphe (aff-Aux "" B)) )

Pour la définition de aff-Aux, il suffit de suivre la spécification de ab-affichage (le préfixe pour les appels récursifs étant égal à la concaténation du préfixe donné et d'un tiret):

(define (ab-affichage B) ;; aff-Aux : Ligne * ArbreBinaire[a] -> Paragraphe ;; (aff-Aux pref B) rend le paragraphe obtenu en préfixant chaque ligne du paragraphe ;; « (ab-affichage B) » par la chaîne «pref» (define (aff-Aux pref B) (if (ab-vide? B) (paragraphe (list (string-append pref "vide"))) (let ((pref2 (string-append pref "-"))) (paragraphe-cons (string-append pref (->string (ab-etiquette B))) (paragraphe-append (aff-Aux pref2 (ab-gauche B)) (aff-Aux pref2 (ab-droit B)))) ) ) ) ;; expression de (ab-affichage B) : (aff-Aux "" B) )

Remarque (efficacité): la structure des deux définitions que nous avons données pour cette fonction sont similaires sauf que la première définition exécute systématiquement en plus, pour chaque appel récursif, un « map » sur les lignes de la représentration (rappelons que le temps de l'exécution d'un map est de l'ordre de la longueur de la liste donnée). Ainsi, la seconde définition est bien plus performante que la première.

Pour s'auto-évaluer
Exercices d'assouplissement