Bloc en Scheme (suite et fin)
Tout d'abord, rappelons les règles de grammaire:
| <bloc> | -> | (let ( <liaison>* ) <corps> ) |
| (let* ( <liaison>* ) <corps> ) | ||
| <liaison> | -> | ( <variable> <expression> ) |
| <corps> | -> | <définition>*<expression> |
et donnons un « exemple »:
(let ((v1 exp1)
(v2 exp2))
(define (f1 ...) corps f1)
(define (f2 ...) corps f2)
expression)
(v2 exp2))
(define (f1 ...) corps f1)
(define (f2 ...) corps f2)
expression)
Précision: nous avons déja dit que l'on ne pouvait pas utiliser les variables liées par les liaisons à l'intérieur des expressions présentes dans les liaisons (par exemple, on ne peut pas utiliser v1 dans exp2). En revanche, on peut utiliser les fonctions définies dans toute la partie des définitions (par exemple, on peut utiliser f1 et f2 dans corps f1 et dans corps f2 pour effectuer une récursivité croisée).
Sémantique
Pour évaluer un bloc -- qui est donc constitué de liaisons, de définitions et d'une expression -- dans un certain environnement que nous nommerons, dans les explications suivantes, environnement courant:
- on évalue, dans l'environnement courant, chacune des expressions présentes dans les liaisons,
- on substitue, dans les définitions et l'expression, chaque variable liée (i.e. présente dans les liaisons) par la valeur de l'expression de sa liason,
- on enrichit l'environnement courant avec les différentes définitions,
- et on évalue, dans ce dernier environnement, l'expression.
Un exemple (uniquement didactique):
(let ((v1 (+ 1 1)) (v2 (+ 1 1 1)))
(define (f1 n) (+ v1 (f2 n)))
(define (f2 n) (* v2 n))
(f1 (+ v1 v2)))
(define (f1 n) (+ v1 (f2 n)))
(define (f2 n) (* v2 n))
(f1 (+ v1 v2)))
dans un premier temps, on évalue (+ 1 1) et (+ 1 1 1) dans l'environnement courant puis on substitue v1 par 2 et v2 par 3 dans les définitions et l'expression. Le bloc est ainsi transformé en:
(define (f1 n) (+ 2 (f2 n)))
(define (f2 n) (* 3 n))
(f1 (+ 2 3)))
(define (f2 n) (* 3 n))
(f1 (+ 2 3)))
les deux définitions enrichissant l'environnement, et on peut alors évaluer, dans ce dernier environnement, l'expression:
| (f1 (+ 2 3)) | --> | (f1 5) |
| --> | (+ 2 (f2 5)) | |
| --> | (+ 2 (* 3 5)) | |
| --> | (+ 2 15) | |
| --> | 17 |
Utilisation
Ainsi un bloc (qui est une expression) est constitué de trois parties
- des liaisons variables --- valeurs,
- des définitions de fonctions,
- une expression.
et toutes les fois où l'on veut
- nommer des valeurs,
- définir des fonctions à l'intérieur d'une expression,
on doit utiliser un bloc.
Exemples
Nous avons déjà vu un grand nombre d'exemples où l'on nomme des valeurs (et nous en verrons deux autres dans le paragraphe suivant), aussi nous ne donnerons que deux exemples, le premier où l'on nomme des valeurs et l'on définit une fonction, le second où l'on ne fait que définir une fonction.
Comme premier exemple, considérons la fonction mult dont nous avons déjà donné une définition (avec map) et écrivons une autre définition, sans utiliser map. Rappelons que, étant donnée une liste de nombres non vide L, cette fonction mult rend la liste obtenue en multipliant tous les éléments de (cdr L) par (car L). Par exemple,
(mult '(3 4 5 6)) -> (12 15 18).
pour écrire une définition de cette fonction, on peut penser
- écrire une fonction interne qui rend la liste voulue,
- pour ce faire, nommer le car de la liste donnée:
;;; mult : LISTE[Nombre]/non vide/ -> LISTE[Nombre]
;;; (mult L) rend la liste obtenue en multipliant tous les éléments de « (cdr L) »
;;; par « (car L) »
(define (mult L)
(let ((facteur (car L)))
;; mult-aux : LISTE[Nombre] -> LISTE[Nombre]
;; (mult-aux L) rend la liste obtenue en multipliant tous les
;; éléments de «L» par «facteur»
(define (mult-aux L)
(if (pair? L)
(cons (* facteur (car L))
(mult-aux (cdr L)))
'()))
(mult-aux (cdr L))))
;;; (mult L) rend la liste obtenue en multipliant tous les éléments de « (cdr L) »
;;; par « (car L) »
(define (mult L)
(let ((facteur (car L)))
;; mult-aux : LISTE[Nombre] -> LISTE[Nombre]
;; (mult-aux L) rend la liste obtenue en multipliant tous les
;; éléments de «L» par «facteur»
(define (mult-aux L)
(if (pair? L)
(cons (* facteur (car L))
(mult-aux (cdr L)))
'()))
(mult-aux (cdr L))))
Comme second exemple (définition d'une fonction à l'intérieur d'une expression), considérons la fonction mult-bis ayant comme spécification:
;;; mult-bis : LISTE[Nombre] -> LISTE[Nombre]
;;; (mult-bis L) rend la liste obtenue en multipliant tous les éléments de «L»
;;; par « (car L) ». Exemples d'applications :
;;; (mult-bis '(2 3 5)) --> (4 6 10)
;;; (mult-bis '()) --> ()
;;; (mult-bis L) rend la liste obtenue en multipliant tous les éléments de «L»
;;; par « (car L) ». Exemples d'applications :
;;; (mult-bis '(2 3 5)) --> (4 6 10)
;;; (mult-bis '()) --> ()
Essayons d'écrire une définition de cette fonction en utilisant l'itérateur map. Comme nous l'avons déjà vu lorsque nous avons implanté la fonction map, pour ce faire, il faut définir une fonction interne qui multiplie sa donnée par (car L). Mais nous ne pouvons pas définir cette fonction directement dans la définition de mult-bis car on ne peut le faire que lorsque la liste n'est pas vide. Pour ce faire, il suffit que la conséquence de l'alternative soit un bloc (et comme nous n'avons pas besoin de nommer de valeur, la partie des liaisons est vide):
(define (mult-bis L)
(if (pair? L)
(let ()
(define (mult-elem e)
(* (car L) e))
(map mult-elem L))
'()))
(if (pair? L)
(let ()
(define (mult-elem e)
(* (car L) e))
(map mult-elem L))
'()))
Bloc et efficacité des programmes
Comme nous l'avons vu, la définition de cette dernière fonction peut très bien être écrite sans bloc (en utilisant map). Nous allons maintenant étudier des fonctions où l'utilisation d'un bloc est très naturelle et où, surtout, elle est gage d'efficacité.
Tout d'abord, reprenons l'exemple du calcul du nombre de racines d'une équation du second degré:
;;; nombre-racines : Nombre * Nombre * Nombre -> nat
;;; (nombre-racines a b c) rend le nombre de racines de l'équation
;;; « a.x**2 + b.x + c = 0 »
(define (nombre-racines a b c)
(let ((delta (- (* b b) (* 4 a c))))
(if (< delta 0)
0
(if (= delta 0)
1
2))))
;;; (nombre-racines a b c) rend le nombre de racines de l'équation
;;; « a.x**2 + b.x + c = 0 »
(define (nombre-racines a b c)
(let ((delta (- (* b b) (* 4 a c))))
(if (< delta 0)
0
(if (= delta 0)
1
2))))
Dans la section , nous avons donné cet exemple en insistant sur le fait que c'était très naturel car nous avons l'habitude d'agir ainsi. Aujourd'hui nous voudrions insister sur l'aspect efficacité: l'utilisation du let permet de ne calculer qu'une fois (au lieu de 2) l'expression (- (* b b) (* 4 a c)).
Bien sûr, dans cet exemple, le gain n'est pas très important, mais nous allons voir maintenant deux autres exemples où le fait de ne pas nommer une valeur qu'on utilise plusieurs fois peut être catastrophique pour l'efficacité.
Premier exemple: nous voudrions tout d'abord écrire une définition de la fonction qui a la spécification suivante:
;;; somme-cumulee-1 : LISTE[Nombre] -> LISTE[Nombre]
;;; (somme-cumulee-1 L) rend la liste dont le premier élément est égal
;;; à la somme des éléments de «L», dont le deuxième élément est égal à
;;; la somme des éléments de « (cdr L) »... dont l'avant dernier élément est égal
;;; au dernier élément de «L» et dont le dernier élément est nul.
;;; Exemple : (somme-cumulee-1 '(1 2 3 4)) --> (10 9 7 4 0)
;;; (somme-cumulee-1 L) rend la liste dont le premier élément est égal
;;; à la somme des éléments de «L», dont le deuxième élément est égal à
;;; la somme des éléments de « (cdr L) »... dont l'avant dernier élément est égal
;;; au dernier élément de «L» et dont le dernier élément est nul.
;;; Exemple : (somme-cumulee-1 '(1 2 3 4)) --> (10 9 7 4 0)
Idée:
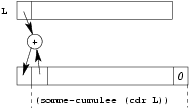
Soit L une liste donnée (dans le dessin ci-dessus, elle est schématisée par le rectangle supérieur) et L-res la liste somme-cumulee-1(L) (dans le dessin ci-dessus, elle est schématisée par le rectangle inférieur). Alors
- (cdr L-res) est égal à (somme-cumulee-1 (cdr L));
- (car L-res) est égal à (+ (car L) (cadr L-res)) soit
à
(+ (car L) (car (somme-cumulee-1 (cdr L)))).
Solution inefficace:
Si l'on écrit comme corps de la fonction somme-cumulee-1 l'expression suivante:
(if (pair? L)
(cons (+ (car L) (car (somme-cumulee-1 (cdr L))))
(somme-cumulee-1 (cdr L)))
'(0))
(cons (+ (car L) (car (somme-cumulee-1 (cdr L))))
(somme-cumulee-1 (cdr L)))
'(0))
pour calculer (somme-cumulee-1 L), il faut calculer deux fois (somme-cumulee-1 (cdr L)). Bonjour l'efficacité! En effet, si l'on nomme tn le temps nécessaire à l'évaluation d'une application de cette fonction sur une liste de longueur n, tn = 2× tn-1 + c: tn est de l'ordre de 2n alors que, visiblement, on peut résoudre ce problème en un temps linéaire comme nous allons le voir maintenant.
Solution efficace:
Il faut nommer la valeur (somme-cumulee-1 (cdr L)). Noter que le bloc ne peut pas être le corps de la définition de la fonction car, pour calculer la valeur, on a besoin de (cdr L) et donc de savoir que la liste n'est pas vide.
(define (somme-cumulee-1 L)
(if (pair? L)
(let ((sc-cdrL (somme-cumulee-1 (cdr L))))
(cons (+ (car L) (car sc-cdrL))
sc-cdrL))
'(0)))
(if (pair? L)
(let ((sc-cdrL (somme-cumulee-1 (cdr L))))
(cons (+ (car L) (car sc-cdrL))
sc-cdrL))
'(0)))
Second exemple: dans l'exemple précédent, nous avons ajouté 0 à la fin de la liste résultat parce que cela facilite l'écriture de la définition. Essayons maintenant d'écrire une définition de la « vraie » fonction somme cumulée:
;;; somme-cumulee : LISTE[Nombre] -> LISTE[Nombre]
;;; (somme-cumulee L) rend la liste dont le premier élément est égal à la
;;; somme des éléments de «L», dont le deuxième élément est égal à la somme
;;; des éléments de « (cdr L) »... dont le dernier élément est égal au dernier
;;; élément de «L». Exemple : (somme-cumulee '(1 2 3 4)) --> (10 9 7 4)
;;; (somme-cumulee L) rend la liste dont le premier élément est égal à la
;;; somme des éléments de «L», dont le deuxième élément est égal à la somme
;;; des éléments de « (cdr L) »... dont le dernier élément est égal au dernier
;;; élément de «L». Exemple : (somme-cumulee '(1 2 3 4)) --> (10 9 7 4)
Pour écrire la définition, le problème est alors que (somme-cumulee (cdr L)) peut être la liste vide (ce qui se passe lorsque (cdr L) est la liste vide). On doit donc exclure ce cas de l'appel récursif:
(define (somme-cumulee0 L)
(if (pair? L)
(if (pair? (cdr L))
(let ((s-cdrL (somme-cumulee0 (cdr L))))
(cons (+ (car L) (car s-cdrL))
s-cdrL))
L)
'()))
(if (pair? L)
(if (pair? (cdr L))
(let ((s-cdrL (somme-cumulee0 (cdr L))))
(cons (+ (car L) (car s-cdrL))
s-cdrL))
L)
'()))
Mais faisons tourner cette définition à la main. On teste si L est la liste vide puis si (cdr L) est la liste vide. Dans le cas contraire, on applique récursivement somme-cumulee0 sur (cdr L), nommons L1 cette valeur. Pour évaluer cette application, on commencera par tester si L1 n'est pas vide; or il ne le sera pas puisque nous avons vu que (cdr L) ne l'était pas. Ce test est donc inutile dans les appels récursifs (mais il l'est au départ).
Comment gérer cela? Il suffit de définir une autre fonction, qui rend la valeur rendue par la fonction que nous définissons, mais que l'on n'appelle que lorsque la liste donnée n'est pas vide. Cette fonction n'est qu'une fonction auxiliaire, aussi nous écrivons sa définition à l'intérieur de la définition demandée:
;;; somme-cumulee : LISTE[Nombre] -> LISTE[Nombre]
;;; (somme-cumulee L) rend la liste dont le premier élément est égal à la
;;; somme des éléments de «L», dont le deuxième élément est égal à la somme
;;; des éléments de « (cdr L) »... dont le dernier élément est égal au dernier
;;; élément de «L». Exemple : (somme-cumulee '(1 2 3 4)) --> (10 9 7 4)
(define (somme-cumulee L)
;; sc-non-vide : LISTE[Nombre]/non vide/ -> LISTE[Nombre]
;; (sc-non-vide L) = (somme-cumulee L)
(define (sc-non-vide L)
(if (pair? (cdr L))
(let ((sc-cdrL (sc-non-vide (cdr L))))
(cons (+ (car L) (car sc-cdrL))
sc-cdrL))
L))
;; expression de somme-cumulee :
(if (pair? L)
(sc-non-vide L)
'()))
;;; (somme-cumulee L) rend la liste dont le premier élément est égal à la
;;; somme des éléments de «L», dont le deuxième élément est égal à la somme
;;; des éléments de « (cdr L) »... dont le dernier élément est égal au dernier
;;; élément de «L». Exemple : (somme-cumulee '(1 2 3 4)) --> (10 9 7 4)
(define (somme-cumulee L)
;; sc-non-vide : LISTE[Nombre]/non vide/ -> LISTE[Nombre]
;; (sc-non-vide L) = (somme-cumulee L)
(define (sc-non-vide L)
(if (pair? (cdr L))
(let ((sc-cdrL (sc-non-vide (cdr L))))
(cons (+ (car L) (car sc-cdrL))
sc-cdrL))
L))
;; expression de somme-cumulee :
(if (pair? L)
(sc-non-vide L)
'()))
| Pour s'auto-évaluer |
|---|
|
|
|
|


