Définition de fonctions internes -- variables globales
Définition de fonctions internes -- variables globales
Définition de fonctions internes
Rappelons les règles de grammaire pour les définitions de fonction:
Ainsi, à l'intérieur d'une définition de fonction, on peut définir d'autres fonctions (on parle alors de fonctions internes). Par exemple, on peut donner une autre définition de la fonction v-cylindre:
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction v-cylindre:
Noter que dans cet environnement, la fonction a-disque n'est pas connue: on ne pourrait pas demander l'évaluation de (a-disque 22). Cela correspond d'ailleurs à l'une des utilisations des définitions internes: toute fonction auxiliaire (i.e. que l'on ne définit que pour écrire la définition d'une fonction) doit être une fonction interne.
Pour évaluer l'application de la fonction v-cylindre,
le reste de l'évaluation est alors simple:
Remarque: à la fin de l'évaluation de l'application de v-cylindre, l'environnement retrouve sa valeur initiale et, à nouveau la fonction a-disque n'est pas définie.
Autres exemples de fonctions internes
Premier exemple: on demande l'évaluation de:
Noter que deux fonctions internes sont définies, au même niveau, dans cet exemple.
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant des définitions, on les ajoute à l'environnement:
l'évaluation de (+ (g 3) (h 3) 1) ne pose alors pas de problème:
Deuxième exemple: on demande l'évaluation de:
Noter que dans cet exemple, une fonction interne (h) est définie à l'intérieur d'une fonction interne (g).
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant une définition (celle de g), on l'ajoute à l'environnement:
Pour l'évaluation de l'application (g 3), on substitue 3 à x dans la définition de g et cette dernière comportant une définition (celle de h), on l'ajoute à l'environnement:
et on subsitue alors 3 à y dans la définition de h:
la fin de l'évaluation est facile et le résultat est:
Troisième exemple: on demande l'évaluation de:
Noter que dans cet exemple, deux fonctions internes (g et h) sont définies à l'intérieur de la fonction f, l'une des fonctions internes (h) étant utilisée dans le corps de l'autre fonction interne (g).
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant deux définitions (celles de g et de h), on les ajoute à l'environnement:
la fin de l'évaluation est facile et le résultat est:
Quatrième exemple: on demande l'évaluation de:
Noter que dans cet exemple, l'application de la fonction f, dont la définition comporte une définittion interne, est une sous-expression de l'application que l'on doit évaluer.
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant une définition (celle de g), on l'ajoute à l'environnement:
Pour l'évaluation de l'application (g 3), on substitue 3 à x dans la définition de g:
l'évaluation (* 3 3) est immédiate:
l'évaluation (+ 9 1) termine l'évaluation de (f 3), aussi après cette évaluation, la définition de la fonction g n'est plus dans l'environnement:
et le résulat est 2:
Notion de variable globale
Dans le paragraphe précédent, nous avons décrit des évaluations d'applications de fonctions dont la définition comporte des définitions internes. Ces définitions sont donc de la forme:
Dans ces exemples, hormis les variations d'environnement, les étapes de l'évaluation sont exactement les memes que lorsque les définitions des fonctions f et g sont au même niveau. Ce n'est pas toujours le cas, comme nous allons voir maintenant.
Premier exemple: donnons une autre définition de la fonction v-cylindre:
Noter que la fonction a-disque est une fonction sans argument (vous avez déjà utilisé de telles fonctions, par exemple (newline) ou (list)).
Noter aussi que dans la définition de la fonction a-disque, il y a la variable r, qui n'est pas une variable de la fonction, mais une variable de la fonction v-cylindre: on dit que r est une variable globale (on dit aussi variable libre) dans la définition de a-disque (et c'est une variable locale (on dit aussi variable liée) pour la définition de v-cylindre). Remarquer enfin que si l'on « sortait » la définition de la fonction a-disque de la définition de v-cylindre, il y aurait une erreur car l'évaluateur ne connaîtrait plus r, la variable globale (mais locale à la définition de v-cylindre).
Comment évalue-t-on l'expression? Cela commence comme dans l'exemple précédent:
et on continue en effectuant de le même façon:
le reste de l'évaluation est alors simple:
Second exemple: reprenons la fonction conc-d et rappelons la définition que nous avons donnée:
Dans la définition précédente, pour tous les appels récursifs, l'argument correspondant à x est toujours le même, celui de l'application initiale de la fonction. Dans cette situation, on peut « globaliser » la variable:
Dans cette définition, x est une variable globale dans la définition de conc-d-x.
Lors de l'évaluation d'une application de conc-d, on commence par enrichir l'environnement en ajoutant la fonction conc-d-x pour la valeur de l'argument correspondant à x et, dans tous les appels récursifs, on n'a pas besoin de transmettre cet argument, il est directement dans la fonction. Par exemple, pour évaluer l'application
(conc-d '(a b) 'c)
on commence par enrichir l'environnement avec la fonction conc-d-x:
(noter le 'c à la place du x) et, dans ce nouvel environnement, on évalue:
(conc-d-x '(a b))
L'évaluation est alors exactement la même que précédemment sauf que toutes les fois où l'on avait (conc-d ... 'c), on a (conc-d-x ...). Autrement dit, on n'a pas besoin de transmettre cet argument à chaque appel récursif car il est mis, une fois pour toutes, dans la définition même de la fonction récursive.
Une autre utilisation des fonctions internes
L'utilisation précédente des fonctions internes -- globalisation de variables -- n'est pas indispensable (mais permet un gain en terme de nombre de substitutions et donc en efficacité). Dans l'exemple du présent paragraphe, l'utilisation d'une fonction interne, avec variable globale, est indispensable.
Nous voudrions écrire une définition de la fonction qui, étant donnée L, une liste non vide de nombres, rend la liste obtenue en multipliant tous les éléments de (cdr L) par (car L). Par exemple,
(mult '(3 4 5 6)) -> (12 15 18).
Comment faire? Si nous devions écrire une fonction qui rend une liste obtenue en multipliant tous les éléments de la liste donnée par une constante, nous utiliserions la fonction map, appliquée à une fonction ad hoc qui rend le produit de sa donnée par la constante. Dans notre problème, on rend la liste obtenue en multipliant tous les éléments de (cdr L) par une valeur; pas de problème, il suffit que la fonction map soit appliquée à (cdr L)! En revanche, le fait que le facteur multiplicatif ne soit pas une constante -- c'est (car L) -- est un problème car cette valeur n'est connue qu'à l'intérieur de l'appel de la fonction mult: on doit donc écrire la définition de la fonction ad hoc -- que nous nommons mult-elem -- soit écrite à l'intérieur de la définition de la fonction mult:
Rappelons les règles de grammaire pour les définitions de fonction:
| <définition> | -> | (define (<nom-fonction><variable>*) <corps> ) |
| <corps> | -> | <définition>*<expression> |
Ainsi, à l'intérieur d'une définition de fonction, on peut définir d'autres fonctions (on parle alors de fonctions internes). Par exemple, on peut donner une autre définition de la fonction v-cylindre:
;;; v-cylindre : Nombre * Nombre -> Nombre
;;; (v-cylindre r h) rend le volume du cylindre de rayon «r»
;;; et de hauteur «h»
(define (v-cylindre r h)
;; a-disque : Nombre -> Nombre
;; (a-disque r) rend la surface du disque de rayon «r»
(define (a-disque r)
(* 3.14 r r))
;; expression de la fonction v-cylindre :
(* (a-disque r) h))
;;; essai de v-cylindre (rend 4559.28) :
(v-cylindre 22 3)
;;; (v-cylindre r h) rend le volume du cylindre de rayon «r»
;;; et de hauteur «h»
(define (v-cylindre r h)
;; a-disque : Nombre -> Nombre
;; (a-disque r) rend la surface du disque de rayon «r»
(define (a-disque r)
(* 3.14 r r))
;; expression de la fonction v-cylindre :
(* (a-disque r) h))
;;; essai de v-cylindre (rend 4559.28) :
(v-cylindre 22 3)
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction v-cylindre:
| Environnement | Évaluation | ||
|
(define (v-cylindre r h)
(define (a-disque r) (* 3.14 r r)) (* (a-disque r) h)) |
(v-cylindre 22 3) --> |
Noter que dans cet environnement, la fonction a-disque n'est pas connue: on ne pourrait pas demander l'évaluation de (a-disque 22). Cela correspond d'ailleurs à l'une des utilisations des définitions internes: toute fonction auxiliaire (i.e. que l'on ne définit que pour écrire la définition d'une fonction) doit être une fonction interne.
Pour évaluer l'application de la fonction v-cylindre,
- comme précédemment, on subsitue dans le corps de la définition de cette fonction les variables par les arguments correspondants,
- en plus, comme il y a une définition interne, on enrichit l'environnement en lui ajoutant la définition de la fonction a-disque:
|
(define (a-disque r)
(* 3.14 r r)) |
(* (a-disque 22) 3)
--> |
le reste de l'évaluation est alors simple:
|
(* (* 3.14 22 22) 3) --> (* 1519.76 3) --> 4559.28 |
Remarque: à la fin de l'évaluation de l'application de v-cylindre, l'environnement retrouve sa valeur initiale et, à nouveau la fonction a-disque n'est pas définie.
Autres exemples de fonctions internes
Premier exemple: on demande l'évaluation de:
(define (f n)
(define (g x)
(+ x x))
(define (h x)
(* x x))
;; expression de (f n) :
(+ (g n) (h n) 1))
(f 3)
(define (g x)
(+ x x))
(define (h x)
(* x x))
;; expression de (f n) :
(+ (g n) (h n) 1))
(f 3)
Noter que deux fonctions internes sont définies, au même niveau, dans cet exemple.
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
| Environnement | Évaluation | ||
|
(define (f n)
(define (g x) (+ x x)) (define (h x) (* x x)) (+ (g n) (h n) 1)) |
(f 3) --> |
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant des définitions, on les ajoute à l'environnement:
|
(define (g x)
(+ x x)) (define (h x) (* x x)) |
(+ (g 3) (h 3) 1) --> --> |
l'évaluation de (+ (g 3) (h 3) 1) ne pose alors pas de problème:
| (+ (+ 3 3) (* 3 3) 1) --> --> |
| (+ 6 9 1) --> |
| 16 |
Deuxième exemple: on demande l'évaluation de:
(define (f n)
(define (g x)
(define (h y)
(+ y 2))
; expression de (g n) :
(* x (h x)))
;; expression de (f n) :
(+ (g n) 1))
(f 3)
(define (g x)
(define (h y)
(+ y 2))
; expression de (g n) :
(* x (h x)))
;; expression de (f n) :
(+ (g n) 1))
(f 3)
Noter que dans cet exemple, une fonction interne (h) est définie à l'intérieur d'une fonction interne (g).
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
| Environnement | Évaluation | ||
|
(define (f n)
(define (g x) (define (h y) (+ y 2)) (* x (h x))) (+ (g n) 1)) |
(f 3) --> |
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant une définition (celle de g), on l'ajoute à l'environnement:
|
(define (g x)
(define (h y) (+ y 2)) (* x (h x))) |
(+ (g 3) 1) --> |
Pour l'évaluation de l'application (g 3), on substitue 3 à x dans la définition de g et cette dernière comportant une définition (celle de h), on l'ajoute à l'environnement:
|
(define (h y)
(+ y 2)) |
(+ (* 3 (h 3)) 1) --> |
et on subsitue alors 3 à y dans la définition de h:
| (+ (* 3 (+ 3 2) ) 1) --> ... |
la fin de l'évaluation est facile et le résultat est:
| --> ... 16 |
Troisième exemple: on demande l'évaluation de:
(define (f n)
(define (g x)
(* x (h x)))
(define (h y)
(+ y 2))
;; expression de (f n) :
(+ (h n) (g n)))
(f 3)
(define (g x)
(* x (h x)))
(define (h y)
(+ y 2))
;; expression de (f n) :
(+ (h n) (g n)))
(f 3)
Noter que dans cet exemple, deux fonctions internes (g et h) sont définies à l'intérieur de la fonction f, l'une des fonctions internes (h) étant utilisée dans le corps de l'autre fonction interne (g).
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
| Environnement | Évaluation | ||
|
(define (f n)
(define (g x) (* x (h x))) (define (h y) (+ y 2)) (+ (h n) (g n))) |
(f 3) --> |
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant deux définitions (celles de g et de h), on les ajoute à l'environnement:
|
(define (g x)
(* x (h x))) (define (h y) (+ y 2)) |
(+ (h 3) (g 3)) --> --> |
- pour l'évaluation de l'application (h 3), on substitue 3 à x dans la définition de h;
- pour l'évaluation de l'application (g 3), on substitue 3 à y dans la définition de g:
| (+ (+ 3 2) (* 3 (h 3) )) --> --> |
- l'évaluation de (+ 3 2) est immédiate;
- pour l'évaluation de l'application (h 3), on substitue 3 à y dans la définition de h:
| (+ 5 (* 3 (+ 3 2) )) --> |
la fin de l'évaluation est facile et le résultat est:
| --> ... 20 |
Quatrième exemple: on demande l'évaluation de:
(define (f n)
(define (g x)
(* x x))
;; expression de (f n) :
(+ (g n) 1))
(/ (f 3) 5)
(define (g x)
(* x x))
;; expression de (f n) :
(+ (g n) 1))
(/ (f 3) 5)
Noter que dans cet exemple, l'application de la fonction f, dont la définition comporte une définittion interne, est une sous-expression de l'application que l'on doit évaluer.
Pour évaluer l'expression donnée, l'environnement ne comporte que la définition de la fonction f:
| Environnement | Évaluation | ||||
|
(define (f n)
(define (g x) (* x x)) (+ (g n) 1)) |
(/ (f 3) 5) --> |
Pour l'évaluation de l'application (f 3), on substitue 3 à n dans la définition de f et cette dernière comportant une définition (celle de g), on l'ajoute à l'environnement:
|
(define (g x)
(* x x)) |

|
(/ (+ (g 3) 1) 5) --> |
Pour l'évaluation de l'application (g 3), on substitue 3 à x dans la définition de g:
| (/ (+ (* 3 3) 1) 5) --> |
l'évaluation (* 3 3) est immédiate:
| (/ (+ 9 1) 5) --> |
l'évaluation (+ 9 1) termine l'évaluation de (f 3), aussi après cette évaluation, la définition de la fonction g n'est plus dans l'environnement:
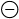
|
(/ 10 5) --> |
et le résulat est 2:
| 2 |
Notion de variable globale
Dans le paragraphe précédent, nous avons décrit des évaluations d'applications de fonctions dont la définition comporte des définitions internes. Ces définitions sont donc de la forme:
(define (f ...)
(define (g ...)
...)
;; expression de f :
...)
(define (g ...)
...)
;; expression de f :
...)
Dans ces exemples, hormis les variations d'environnement, les étapes de l'évaluation sont exactement les memes que lorsque les définitions des fonctions f et g sont au même niveau. Ce n'est pas toujours le cas, comme nous allons voir maintenant.
Premier exemple: donnons une autre définition de la fonction v-cylindre:
;;; v-cylindre : Nombre * Nombre -> Nombre
;;; (v-cylindre r h) rend le volume du cylindre de rayon «r»
;;; et de hauteur «h»
(define (v-cylindre r h)
;; a-disque : Nombre -> Nombre
;; (a-disque r) rend la surface du disque de rayon «r»
(define (a-disque)
(* 3.14 r r))
;; expression de la fonction v-cylindre :
(* (a-disque) h))
;;; essai de v-cylindre (rend 4559.28) :
(v-cylindre 22 3)
;;; (v-cylindre r h) rend le volume du cylindre de rayon «r»
;;; et de hauteur «h»
(define (v-cylindre r h)
;; a-disque : Nombre -> Nombre
;; (a-disque r) rend la surface du disque de rayon «r»
(define (a-disque)
(* 3.14 r r))
;; expression de la fonction v-cylindre :
(* (a-disque) h))
;;; essai de v-cylindre (rend 4559.28) :
(v-cylindre 22 3)
Noter que la fonction a-disque est une fonction sans argument (vous avez déjà utilisé de telles fonctions, par exemple (newline) ou (list)).
Noter aussi que dans la définition de la fonction a-disque, il y a la variable r, qui n'est pas une variable de la fonction, mais une variable de la fonction v-cylindre: on dit que r est une variable globale (on dit aussi variable libre) dans la définition de a-disque (et c'est une variable locale (on dit aussi variable liée) pour la définition de v-cylindre). Remarquer enfin que si l'on « sortait » la définition de la fonction a-disque de la définition de v-cylindre, il y aurait une erreur car l'évaluateur ne connaîtrait plus r, la variable globale (mais locale à la définition de v-cylindre).
Comment évalue-t-on l'expression? Cela commence comme dans l'exemple précédent:
| Environnement | Évaluation | ||
|
(define (v-cylindre r h)
(define (a-disque) (* 3.14 r r)) (* (a-disque) h)) |
(v-cylindre 22 3)
--> |
et on continue en effectuant de le même façon:
- on subsitue dans le corps de la définition de cette fonction les variables, qui ne sont pas locales à des définitions internes, par les arguments correspondants,
- en plus, comme il y a une définition interne, on enrichit l'environnement en lui ajoutant la définition de la fonction a-disque dans laquelle on a substitué 22 à r puisque r est une variable globale dans la définition de a-disque:
|
(define (a-disque)
(* 3.14 22 22)) |
(* (a-disque) 3) |
le reste de l'évaluation est alors simple:
|
--> (* (* 3.14 22 22) 3) --> (* 1519.76 3) --> 4559.28 |
Second exemple: reprenons la fonction conc-d et rappelons la définition que nous avons donnée:
(define (conc-d L x)
(if (pair? L)
(cons (car L) (conc-d (cdr L) x))
(list x)))
(if (pair? L)
(cons (car L) (conc-d (cdr L) x))
(list x)))
Dans la définition précédente, pour tous les appels récursifs, l'argument correspondant à x est toujours le même, celui de l'application initiale de la fonction. Dans cette situation, on peut « globaliser » la variable:
;;; conc-d : LISTE[alpha] * alpha -> LISTE[alpha]
;;; (conc-d L x) rend la liste obtenue en ajoutant «x» à la fin de la liste «L»
(define (conc-d L x)
;; conc-d-x : LISTE[alpha] -> LISTE[alpha]
;; (conc-d-x L) rend la liste obtenue en ajoutant «x» à la fin de la liste «L»
(define (conc-d-x L)
(if (pair? L)
(cons (car L) (conc-d-x (cdr L)))
(list x)))
(conc-d-x L))
;;; (conc-d L x) rend la liste obtenue en ajoutant «x» à la fin de la liste «L»
(define (conc-d L x)
;; conc-d-x : LISTE[alpha] -> LISTE[alpha]
;; (conc-d-x L) rend la liste obtenue en ajoutant «x» à la fin de la liste «L»
(define (conc-d-x L)
(if (pair? L)
(cons (car L) (conc-d-x (cdr L)))
(list x)))
(conc-d-x L))
Dans cette définition, x est une variable globale dans la définition de conc-d-x.
Lors de l'évaluation d'une application de conc-d, on commence par enrichir l'environnement en ajoutant la fonction conc-d-x pour la valeur de l'argument correspondant à x et, dans tous les appels récursifs, on n'a pas besoin de transmettre cet argument, il est directement dans la fonction. Par exemple, pour évaluer l'application
(conc-d '(a b) 'c)
on commence par enrichir l'environnement avec la fonction conc-d-x:
(define (conc-d-x L)
(if (pair? L)
(cons (car L) (conc-d-x (cdr L)))
(list 'c)))
(if (pair? L)
(cons (car L) (conc-d-x (cdr L)))
(list 'c)))
(noter le 'c à la place du x) et, dans ce nouvel environnement, on évalue:
(conc-d-x '(a b))
L'évaluation est alors exactement la même que précédemment sauf que toutes les fois où l'on avait (conc-d ... 'c), on a (conc-d-x ...). Autrement dit, on n'a pas besoin de transmettre cet argument à chaque appel récursif car il est mis, une fois pour toutes, dans la définition même de la fonction récursive.
Une autre utilisation des fonctions internes
L'utilisation précédente des fonctions internes -- globalisation de variables -- n'est pas indispensable (mais permet un gain en terme de nombre de substitutions et donc en efficacité). Dans l'exemple du présent paragraphe, l'utilisation d'une fonction interne, avec variable globale, est indispensable.
Nous voudrions écrire une définition de la fonction qui, étant donnée L, une liste non vide de nombres, rend la liste obtenue en multipliant tous les éléments de (cdr L) par (car L). Par exemple,
(mult '(3 4 5 6)) -> (12 15 18).
Comment faire? Si nous devions écrire une fonction qui rend une liste obtenue en multipliant tous les éléments de la liste donnée par une constante, nous utiliserions la fonction map, appliquée à une fonction ad hoc qui rend le produit de sa donnée par la constante. Dans notre problème, on rend la liste obtenue en multipliant tous les éléments de (cdr L) par une valeur; pas de problème, il suffit que la fonction map soit appliquée à (cdr L)! En revanche, le fait que le facteur multiplicatif ne soit pas une constante -- c'est (car L) -- est un problème car cette valeur n'est connue qu'à l'intérieur de l'appel de la fonction mult: on doit donc écrire la définition de la fonction ad hoc -- que nous nommons mult-elem -- soit écrite à l'intérieur de la définition de la fonction mult:
;;; mult : LISTE[Nombre]/non vide/ -> LISTE[Nombre]
;;; (mult L) rend la liste obtenue en multipliant tous les éléments de « (cdr L) »
;;; par « (car L) »
(define (mult L)
;; mult-elem : Nombre -> Nombre
;; (mult-elem e) rend « (* (car L) e) »
(define (mult-elem e)
(* (car L) e))
;; expression de la définition de (mult L) :
(map mult-elem (cdr L)))
;;; (mult L) rend la liste obtenue en multipliant tous les éléments de « (cdr L) »
;;; par « (car L) »
(define (mult L)
;; mult-elem : Nombre -> Nombre
;; (mult-elem e) rend « (* (car L) e) »
(define (mult-elem e)
(* (car L) e))
;; expression de la définition de (mult L) :
(map mult-elem (cdr L)))
| Pour s'auto-évaluer |
|---|
|
|


